这几天感觉知识的海洋真的是无边无际的，一旦查资料就意味着要查更多的资料，不懂的东西简直一个接着一个。希望某天能对这些知识有个大概的把握吧，废话不多说，开始积累！
References：
电子文献：
https://www.cnblogs.com/hrlnw/archive/2013/08/06/2826651.html
https://www.cnblogs.com/zyly/p/9651261.html
https://baike.baidu.com/item/HOG/9738560?fr=aladdin
https://zhuanlan.zhihu.com/p/40960756
https://www.jianshu.com/p/354acdcbae3f
https://blog.csdn.net/xjp_xujiping/article/details/89430002
https://www.leiphone.com/news/201708/ZKsGd2JRKr766wEd.html
参考文献：
[1]Histograms of Oriented Gradients for Human Detection
[2]Understanding and Diagnosing Visual Tracking Systems
特征描述子
特征描述子就是图像的一种表示，这种表示抽取了有用的信息，丢掉了不相关的信息。通常特征描述子会把一个WxHx3（3个channel）的图像转换成一个向量或者一个矩阵。
HOG特征
HOG（Histogram of Oriented Gradient），中文译为方向梯度直方图。它是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子，通过计算像局部区域中不同方向上梯度的值，然后进行累积，得到代表这块区域特征的直方图，可将其输入到分类器里面进行目标检测。
下面是论文中所呈现的进行人物检测时所采用的特征提取与目标检测的流程，本文将主要分析特征提取的部分（论文中对运用SVM分类器做检测的部分分析甚少，因此不做重点）。
思想
HOG特征的主要思想是：在图像中，局部目标的表象和形状能够被梯度或边缘的方向密度分布很好地描述。由于，梯度主要存在于边缘的地方，因此其密度分布能一定程度上描述目标物体的形状等特征。
思路
在介绍HOG特征提取的基本思路之前，我先放一张图，我认为先了解block和cell有助于理解思路，否则有点抽象，可能会（像我当初一样）看得很迷。下图的分割尺度与后文的分析一致，即一个block分成2x2的cell，一个cell分成8x8的pixel，可以先记下来。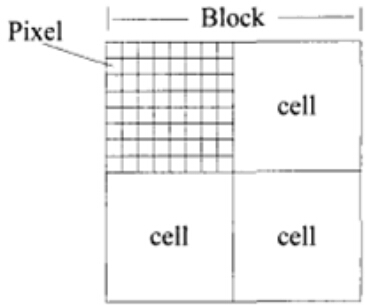
HOG特征提取的基本思路是：
- 为了减少光照因素的影响，首先需要将整个图像进行归一化，这种压缩处理能够有效地降低图像局部的阴影和光照变化。
- 将图像分成很多小的cell，采集cell中各像素点梯度的幅值和方向，然后在每个cell中统计出一个一维的梯度方向直方图。
- 为了对光照和阴影有更好的不变性，我们可以在更大的范围内，对block进行对比度归一化。
- 在归一化后，最终获得的即为HOG描述子。
这里共做了两次normalization，不要搞混了。
那么，为什么要分成很多小的cell呢？因为用特征描述子的一个主要原因是它提供了一种紧凑的压缩表示。后面我们会看到如何把一个9个bin的直方图表示成9个数的数组。此外，对每个cell统计梯度直方图不仅可以使表示压缩而紧凑，用直方图来表示一个patch还可以使其可以更加抗噪，因为一个gradient可能会有噪音，但是用直方图来表示后就不会对噪音那么敏感了。
流程
Normalize gamma ＆ colour
由于在图像的纹理强度中，局部的表层曝光贡献的比重比较大，因此为了减少光照因素的影响，我们首先采用Gamma校正法对输入图像的颜色空间进行归一化。
Gamma校正可以提高图像中偏暗或者偏亮部分的对比效果，能有效降低图像局部的阴影和光照变化。其校正公式为：其中$I$为图像像素值，$\gamma$为校正系数。
由幂函数的性质容易推得Gamma校正的作用，这里以灰度图像（即仅有黑白，单通道）为例做一个简单解释。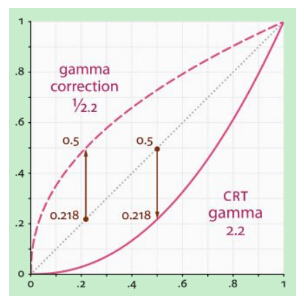
当$\gamma$小于1时，在低灰度值区域内，动态范围变大，图像对比度增强；在高灰度值区域，动态范围变小，图像对比度降低。图像的整体灰度值变大，如下面中间的图片（左边是原图）。
当$\gamma$大于1时，在低灰度值区域内，动态范围变小，图像对比度降低；在高灰度值区域，动态范围变大，图像对比度提高。图像的整体灰度值变小，如下面右边的图片。
注：灰度值也称灰度等级，范围一般从0到255，白色为255，黑色为0。
然而，是否使用Gamma校正还要视具体情况而定，当涉及大量的类内颜色变化时，比如斑马等自身就颜色变化丰富的物体，不校正效果会更好。
上面的例子使用的是灰度图像，事实上，RGB彩色图（三通道）的performance会更好一些。可以看一下下面的对比图。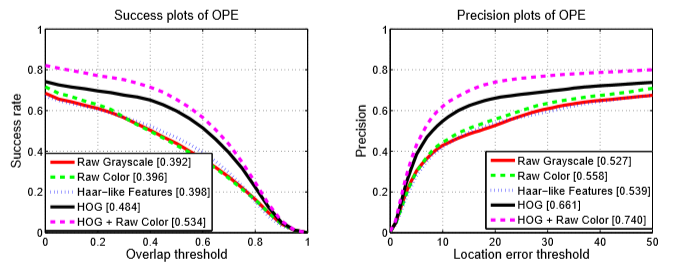
Image segmentation
分割图像这一步在论文的流程图中没有，我觉得有必要说一下，因此自行添加了一步。
这里先说一下为什么要进行图像分割。如果对一大幅图片直接提取特征，往往得不到好的效果。因为如果提取区域比较大，那么两个完全不同的图像，也可能提取出相似的HOG特征。但这种可能性在较小的区域就很小。此外，当我们把图像分割成很多区块（patch）然后对每个区块提取特征时，这其中也包含了几何上的位置特性。例如，正面的人脸，左上部分的图像区块提取的HOG特征一般是和眼睛的HOG特征相符合的。
HOG的图像分割策略一般有overlap和non-overlap两种，如下图所示。第一张图是overlap的情况，指的是分割出的区块会有互相重合的区域。而non-overlap指的是区块不交叠，没有重合区域。
overlap的优点在于这种分割方式可以防止对一些物体的切割，例如，如果分割的时候正好把一个眼睛从中间切割分到了两个patch中，那么提取完HOG特征之后，可能会影响接下来的分类效果。但是如果两个patch之间有一个overlap，那么这里的三个patch至少有一个内会保留完整的眼睛。overlap的缺点在于计算量大，因为重叠区域的像素需要重复计算。
non-overlap恰恰相反，其缺点如上所述，就是有时会将一个连续的物体切割开，得到不太好的HOG特征。但它的优点是计算量小，尤其是与图像金字塔（Image Pyramid，详见computer-vision笔记：图像金字塔与高斯滤波器）相结合时，这个优点更为明显。
在这里，我们用overlap的策略将图像分割成一个个互相重叠的block。也就是说，每个cell的直方图都会被多次用于最终的特征描述子的计算。虽然这看起来有冗余，但可以显著地提升性能。
Compute gradients
接下来就是计算图像每个像素点梯度。$G_{y}\left ( x,y \right )$算法同理。
在具体实现时，我们可以使用如下两种kernel来实现上面梯度的计算。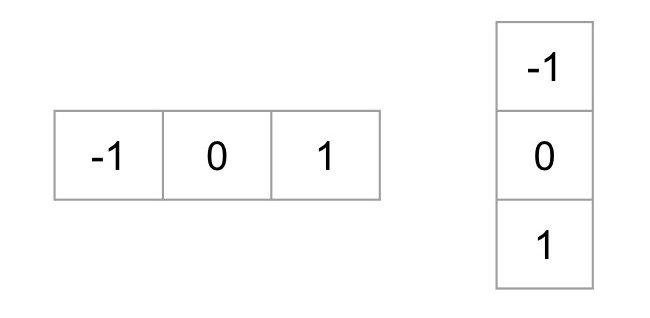
接着计算梯度的幅值和方向。
可以看到，图像的梯度去掉了很多不必要的信息（比如不变的背景色），并且加重了轮廓。Weighted vote into spatial ＆ orientation cells
将图像划分成小的cell（矩形或者环形），然后统计每一个cell的梯度直方图，即可以得到一个cell的描述符。
注意，这里我们在一个block内划分4个cell，即2×2个cell组成一个block，8x8个像素点组成一个cell。将一个block内每个cell的描述符串联起来即可得到一个block的HOG描述符。
我们先来看一下各个像素点的梯度的具体计算情况。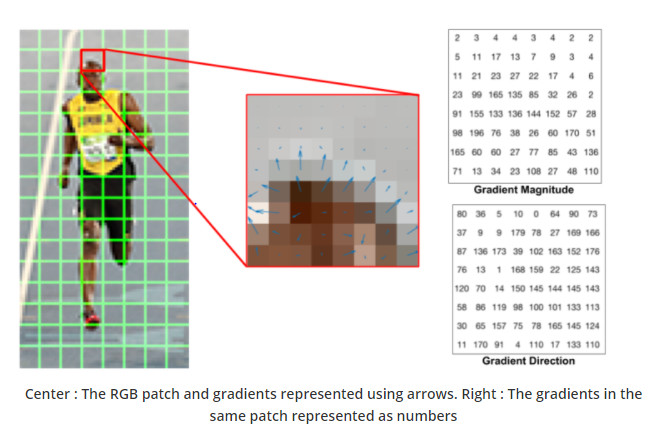
统计梯度直方图的方式是利用刚才计算得出的cell中每一个像素点的梯度进行加权投票。我们一般考虑采用9个bin的直方图来统计一个cell中像素的梯度信息，即将cell的梯度方向0~180°（无向）或0~360°（考虑正负）分成9个bin，如下图所示： 
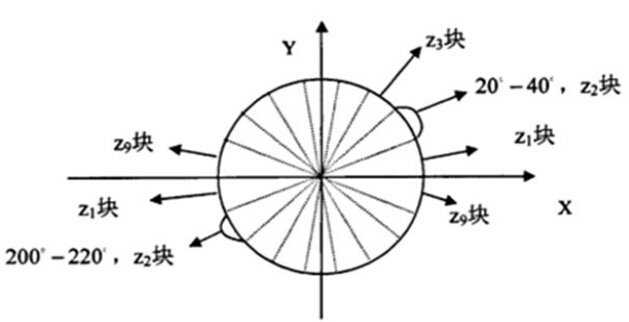如果cell中某一像素的梯度方向是20~40°，那么上面这个直方图第2个bin的计数就要加1，这样对cell中的每一个像素用梯度方向在直方图中进行加权投影（权值大小等于梯度幅值），将其映射到对应角度范围的bin内，就可以得到这个cell的梯度方向直方图了，即该cell对应的一个9维特征向量。若梯度方向位于相邻bin的交界处（如20°、40°等），需要对其进行方向和位置上的双线性插值。 
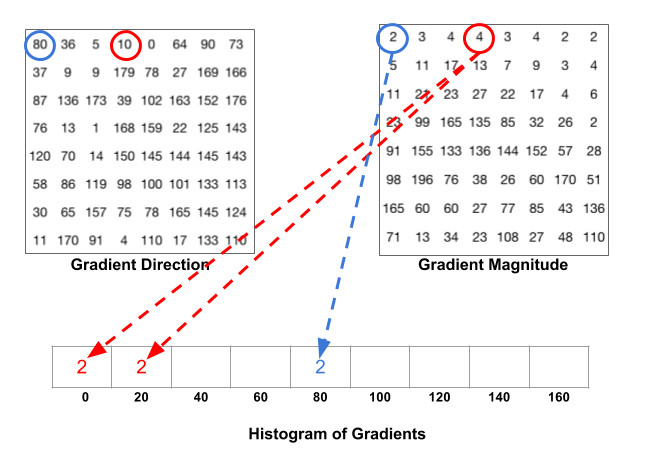上图是一个比较直观的加权投票的演示，这里将投影在交界处的梯度的幅值对半分至两侧的bin。
要注意的是，如果一个角度大于160度，也就是在160至180度之间，我们知道这里角度0和180度是一样的，所以在下面这个例子里，像素的角度为165度时，就要把幅值按照比例放到0和160的bin里面去，也就是上面说的双线性插值。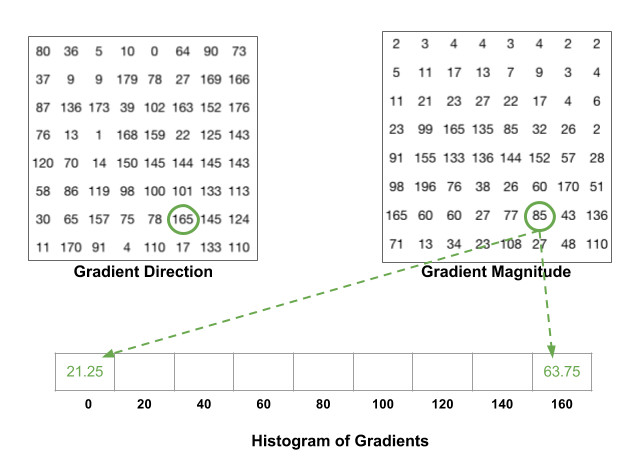
事实上，我们可以采用幅值本身或者它的函数（幅值的平方根、幅值的平方、幅值的截断形式）来表示权值，但经实际测试表明：使用幅值来表示权值能获得最佳的效果。采用梯度幅值作为权重，可以使那些比较明显的边缘的方向信息对特征表达影响增大，这样比较合理，因为HOG特征主要就是依靠这些边缘纹理。
经实验还发现，采用无向的梯度（即0~180°）和9个bin的直方图，能在行人检测试验中取得最佳的效果。Contrast normalize over overlapping spatial blocks
由于局部光照的变化，以及前景背景对比度的变化，使得梯度强度的变化范围非常大，这就需要对梯度做局部对比度归一化。归一化能够进一步对光照、阴影、边缘进行压缩，使得特征向量对光照、阴影和边缘变化具有鲁棒性。
我们之前已将2x2的cell组成了更大的block，现在要做的就是针对每个block进行对比度归一化。
通常使用的HOG结构大致有三种：矩形HOG（R-HOG），圆形HOG（C-HOG）和中心环绕HOG。它们的单位都是block。实验证明，矩形HOG和圆形HOG的检测效果基本一致，而环绕形HOG效果相对差一些。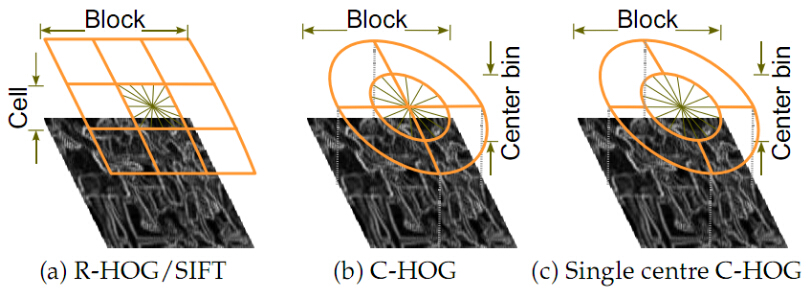
我们一般根据如下公式对block进行对比度归一化：这里$v$是该block未经归一化的特征向量，比如这里一个block含2x2个cell，每个cell对应一个9维的特征向量，那么这个block的特征向量的长度就是2x2x9。这里$\xi$是一个很小的数，主要是为了防止分母等于零而引入的。Collect HOG’s over detection window
我们先review一下，上面我们首先把样本图片分割为若干个像素的cell，然后把梯度方向划分为9个区间，在每个cell里面对所有像素的梯度方向在各个区间进行直方图统计，得到一个9维的特征向量；然后我们使每相邻4个cell构成一个block，把一个block内的特征向量串联起来得到一个36（即2x2x9）维的特征向量。
接下来，我们用block对样本图像进行扫描，stride为一个cell的大小，扫描完成后，我们将扫描过程中每个block的特征向量（即上述36维的）串联起来，得到样本的特征向量，也就是可以输入到后面分类器的HOG特征描述子。
如此，就完成了HOG特征的提取。
我们可以可视化一下最后的HOG特征，可见主要捕捉的是博尔特的躯干和腿。
总结
优点
- HOG特性能较好地捕捉局部形状信息，对几何和光学变化都有很好的不变性。
- HOG特征是在密集采样的图像块中求取的，在计算得到的HOG特征向量中隐含了该块与检测窗口之间的几何空间位置关系。
不足
- 很难处理遮挡问题，人体姿势动作幅度过大或物体方向改变时不易检测（这个问题后来在DPM中采用可变形部件模型的方法得到了改善）。
- 没有选取主方向，也没有旋转梯度方向直方图，因而本身不具有旋转不变性（较大的方向变化），其旋转不变性是通过采用不同旋转方向的训练样本来实现的。
- 本身不具有尺度不变性，其尺度不变性是通过缩放检测窗口图像的大小（如Image Pyramid）来实现的。
- 由于梯度的性质，HOG对噪点相当敏感，在实际应用中，在block和cell划分之后，对于得到各个区域，有时候还会做一次高斯平滑去除噪点。但又由于HOG特征是基于边缘的，平滑操作会降低边缘信息的对比度，从而减少图像中的有用信息，因此还需好好做个balance。
FHOG
由于后续的研究发现HOG特征可以降维。因此在HOG的基础上，又提出了FHOG（我理解为fast HOG），也取得了广泛的应用。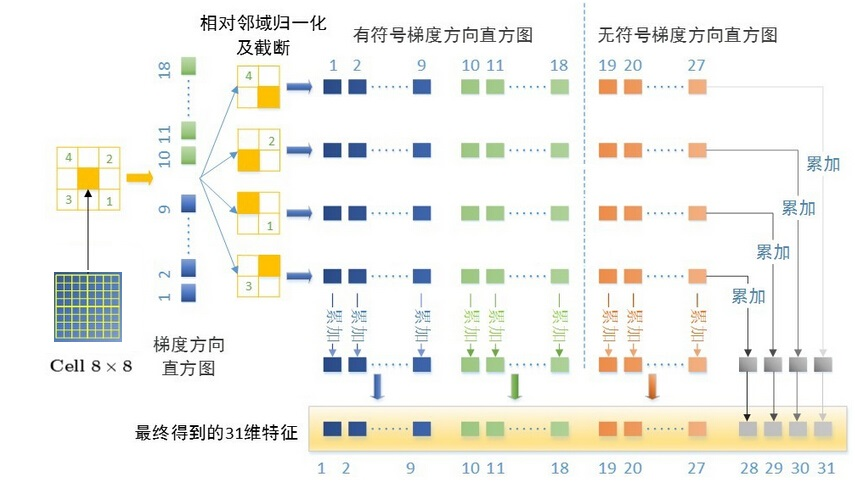
计算机视觉女神
或许会发现本文中好多的图例都用了同一位女士的脸，这里就扯点题外话。
照片中的女子名为Lena Soderberg，对计算机视觉领域有一定的接触的朋友应该对这张照片不会陌生。这张照片是标准的数字图像处理用例，各种算法研究经常会使用这张图作为模板。那为什么要用这幅图呢？
David C. Munson在“A Note on Lena”中给出了两条理由：
- 首先，该图像中各个频段的能量都很丰富，既有低频（光滑的皮肤），也有高频（帽子上的羽毛），适度地混合了细节、平滑区域、阴影和纹理，很适合来测试各种图像处理算法。
- 其次，Lena是位迷人的女子，能有效吸引研究者（大部分为男性）做研究。
该照片其实是一张于1972年11月出版的Playboy的中间插页。1973年，南加州大学信号图像处理研究所的副教授Alexander和学生一起，为了一个同事的学会论文正忙于寻找一幅好的图片。他们想要一幅具有良好动态范围的人的面部图片用于扫描。这时，不知是谁拿着一本Playboy走进研究室。由于当时实验室里使用的扫描仪（Muirhead wirephoto scanner）分辨率是100行每英寸，试验也仅仅需要一副512X512的图片，所以他们只将图片顶端开始的5.12英寸扫描下来，并切掉肩膀以下的部分。多年以来，由于图像Lena源于Playboy，将其引用于科技文章中饱受争议。Playboy杂志也将未授权的引用告上法庭。但随着时间的流逝，人们渐渐淡忘Lena的来源，Playboy也放松了对此的关注。值得一提的是，Lena也是Playboy发行的最畅销的海报，已经出售7,161,561份。其真正刊登的原图如下。
1997年，在图像科学和技术协会的第50届会议上，Lenna被邀为贵宾出席。在会议上，她忙于签名、拍照以及介绍自我。
说实话每次看到这张照片，想起学术界那些大牛们居然能弄出这样一个挺有意思的故事，不免觉得也挺有趣的。在我最喜欢的美剧之一《Silicon Valley》中，也有计算机视觉女神的身影。
重温大结局的时候发现也出现了。
大家对计算机视觉有兴趣的话，其实自己也打印一张摆墙上，这样就可以和懂的小伙伴们一起讨论问题了。