computer vision笔记：相关滤波与KCF

相关滤波（cross-correlation）是在目标跟踪领域一种非常强大的方法，主打简洁和高速，各种基于相关滤波的算法层出不穷。其中，KCF（不是肯德基）是一个非常经典的算法，在目标跟踪领域虽说它不是最早运用相关滤波的算法（MOSSE要早于它），但是它对之后运用相关滤波进行目标跟踪的这一系列算法有重要的奠基作用。本文就最近对这些方面的了解，结合自己的思考，做一个简单的整理归纳，如有疏漏之处还请多多指教。

References：

电子文献：
https://blog.csdn.net/fhcfhc1112/article/details/83783588
https://blog.csdn.net/weixin_39467358/article/details/83304082
https://www.cnblogs.com/jins-note/p/10215511.html
https://blog.csdn.net/li_dongxuan/article/details/70667137?locationNum=5&fps=1
https://www.leiphone.com/news/201709/kLil97MnXF8Gh3sC.html

参考文献：
[1]High-Speed Tracking with Kernelized Correlation Filters
[2]Visual Object Tracking using Adaptive Correlation Filters
[3]Exploiting the Circulant Structure of Tracking-by-detection with Kernels

---

建议

由于KCF这篇文章主要是从理论上面来论述相关滤波来做tracking，其中涉及数学、理论的东西还是挺繁琐的。因此在正文开始之前，推荐可以先看一下我之前总结的几篇有关的博文，后文涉及到的话就不详细写了。
循环矩阵：linear-algebra笔记：循环矩阵。
HOG特征：computer-vision笔记：HOG特征。
正负样本：machine-learning笔记：数据采样之正样本和负样本。
闭式解：machine-learning笔记：闭式解。
此外，还可以先看看b站up主桥本环关于相关滤波两个算法的讲解视频目标跟踪：相关滤波算法MOSSE实现代码讲解和目标跟踪：相关滤波算法KCF实现代码讲解，个人觉得讲得挺不错的。

---

论文

这里分别是MOSSE和KCF两个算法的论文，我在阅读时已用黄色高亮一部分重点。同时本篇文章也主要参考了这两篇paper，可以先看，也可以看完本文再看。

---

相关滤波

先来看一个公式：

$$\left ( f\star g \right )\left ( \tau \right ):=\int_{-\infty }^{\infty }f^{\ast }\left ( t \right )g\left ( t+\tau \right )dt$$

这里$:=$表示“定义为”（等效于等号上加个delta或者def），$\ast$表示复数共轭（complex-conjugate），而这里的$\star$表示的就是相关滤波操作。
你可能会觉得这个式子非常熟悉，是的，它非常像卷积的式子。但是不同的是，一般的卷积操作为$\int_{-\infty }^{\infty }f\left ( t \right )g\left ( t-\tau \right )dt$，而在相关滤波这里是加号。这就是说，在卷积的时候，我们需要把模板先进行翻转，再进行卷积，而相关操作就不需要了。
其实相关操作就是用来衡量两个信号是否相关，当两个信号越相似、相关性越强的时候，他们做相关操作输出的响应就会越强。用到目标跟踪里面，当做相关操作的两个框中的目标越相似，我们就会获得越高的响应。
相关滤波的实际意义是把输入图像映射到一个理想响应图，将这个响应图当中的最高峰与目标中心点对应起来，也就是我们预测的目标接下来的位置。它一个最主要的优点就是能够借助于傅里叶变换，从而快速计算大量的候选样本的响应值。

---

循环矩阵

在论文High-Speed Tracking with Kernelized Correlation Filters的introduction部分，有这样一句话：“we argue that undersampling negatives is the main factor inhibiting performance in tracking.”也就是说，负样本的欠采样是阻碍跟踪效果的主要因素。这在之前的文章中介绍过，这里就不在细述了。
这句话主要针对的问题是我们可以从一张图像中获得几乎无限的负样本。但由于跟踪的时间敏感性，我们的跟踪算法只能在尽可能多地采集样本和维持较低的计算需求之间取得一个平衡。之前通常的做法是从每一帧中随机选择几个样本。
KCF的一大贡献就是采用了一种更方便的方法迅速获取更多的负样本，以便于能够训练出一个更好的分类器。作者发现，在傅里叶域中，如果我们使用特定的模型进行转换，一些学习算法实际上变得更容易（in the Fourier domain, some learning algorithms actually become easier as we add more samples, if we use a specific model for translations）。
具体的做法如下，首先利用一个n维列向量来表示目标，记为$x$，然后利用$x$和一个循环移位矩阵$P$生成一个循环矩阵，其目的是使用一个base sample（正样本）和生成多个虚拟样本（负样本）来训练一个分类器。


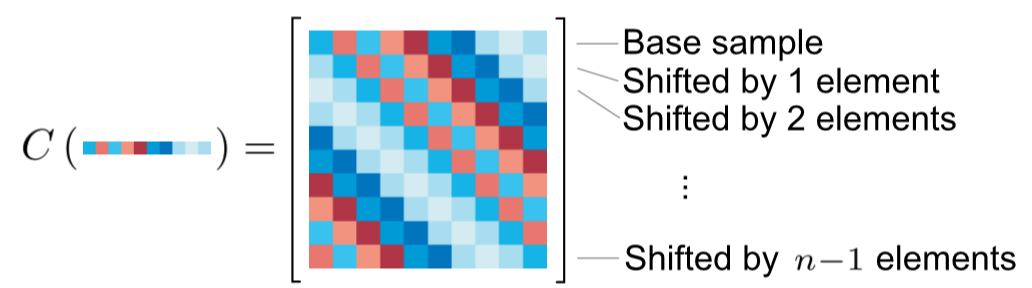
根据循环特性可以推出下面两点：

1. 可以周期性的获得同样的信号。
2. 同样的，我们可以把上面的变换等效成将base sample即生成向量正向移动一半长度和反向移动一半长度组合而成。

这里是一个循环图片的示例，使用base sample，若我们向下移动15个像素，也就是从下面剪切15个像素拼到上面，就会变成左二图，若移动30个就可以生成左一图，右侧的图片是上移生成的。这就是在做tracking时循环采样的样本，一般会在目标周围取一个比目标更大的一个框，然后对大框框取的图像区域进行循环采样，那么就会生成这样一些新的样本来模拟我们的正样本并用于训练。

注意：这些新样本称为虚拟样本，不属于正样本但可以用于回归训练。

获得了这样一个循环矩阵之后，作者接下来说：“all circulant matrices are made diagonal by the Discrete Fourier Transform(DFT), regardless of the generating vector x.”就是说循环矩阵的生成向量是完全指定的，且循环矩阵有一个非常好的性质：对任意生成向量$\widehat{x}$，我们都可以通过离散傅立叶变换（具有线性性）对循环矩阵进行对角化表示。

$$X=C(x)=F\cdot diag(\widehat{x})\cdot F^{H}$$

这里的$F$是一个与向量$\widehat{x}$无关的常数矩阵，如果这里看得不懂的话，可以参照linear-algebra笔记：循环矩阵。
如此，在傅里叶域内，用离散傅里叶变换来做之后的计算，对速度会有非常大的提升。
用到循环矩阵后，有两个常用的公式，可以参考我之前的文章。

---

训练

KCF做训练时所用的是岭回归。在线性情况下，岭回归的优化目标方程如下所示：

$$f\left ( z \right )=w^{T}z$$ $$\underset{w}{min}\sum_{i}\left ( f\left ( x_{i}-y_{i} \right ) \right )^{2}+\lambda \left \| w \right \|^{2}$$

其闭式解为：

$$w=\left ( X^{T}X+\lambda I \right )^{-1}X^{T}y$$

此时就可以利用循环矩阵在傅里叶域计算的性质来求解了。最后求出如下式子：

$$F\left ( w \right )=\frac{\widehat{x}}{\widehat{x}\odot \widehat{x}^{\ast }+\lambda \delta }\odot F\left ( y \right )=\frac{\widehat{x}\odot \widehat{y}}{\widehat{x}\odot \widehat{x}^{\ast }+\lambda \delta }$$

从原来的矩阵相乘和求逆，转换到傅里叶域的点乘和点除（这里的除号是点除），一下子运算就简单了许多。
在非线形的情况下，也可以得到一个同样的情况，这里需要引入一个满足条件的核，例如高斯核、线性核等，最后可计算得出一个闭式解。

非线性情况下，引入核可得到一个类似的岭回归的优化目标方程：

$$w=\sum_{i}\alpha _{i}\varphi \left ( x_{i} \right )$$ $$f\left ( z \right )=w^{T}z=\sum_{i=1}^{n}\alpha _{i}\kappa \left ( z,x_{i} \right )$$ $$\underset{w}{min}\sum_{i}\left ( f\left ( x_{i}-y_{i} \right ) \right )^{2}+\lambda \left \| w \right \|^{2}$$

这里我们定义核函数$\kappa$为基向量$\varphi \left ( x \right )$之间的点积，即$\varphi^{T} \left ( x \right )\varphi \left ( x{}’ \right )=\kappa \left ( x,x{}’ \right )$。
在岭回归/脊回归（Ridge Regression）中，闭式解的基本形式如下：

$$\alpha =\left ( K+\lambda I \right )^{-1}y$$

这里$K$表示核空间的核矩阵，由核函数得到$K_{ij}=\kappa \left ( x_{i},x_{j} \right )=\varphi \left ( X \right )\varphi \left ( X \right )^{T}$。
最终可得：

$$\widehat{\alpha }=\frac{\widehat{y}}{\widehat{k}^{xx}+\lambda }$$

这里的除号也是点除，此时求出来的$K$和$\alpha$就可以来做tracking了。同样的，我们还是利用循环矩阵的性质并且在傅里叶域内来做计算。

---

快速检测

我们很少希望单独来评估一个图像块的回归函数$f\left ( z \right )$。为了检测感兴趣的目标对象，我们通常希望在几个图像位置上评估$f\left ( z \right )$，这几个候选块（candidate patches）可以通过循环移位来建模。
定义$K^{z}$表示所有训练样本和所有候选块之间的核矩阵$K^{z}=\varphi \left ( X \right )\varphi \left ( Z \right )^{T}$。由于样本和图像块都是分别通过基础样本$x$和基础图像块$z$的循环移位组成的，因此矩阵$K^{z}$的每个元素可以表示为：$K_{i,j}=k(P^{i-1}z,P^{j-1}x)$。这里的$P$表示的是位移矩阵。易验证，$K^{z}$也是循环矩阵。
可计算得到各测试样本的响应值：

$$f\left ( z \right )=\left ( K^{z} \right )^{T}\alpha$$ $$\widehat{f}\left ( z \right )=\widehat{k}^{xz}\odot \widehat{\alpha }$$

最后，我们可以求得一张feature map，也就是一张二维的响应图。

---

附录

这里补充在原论文的appendix中提到的两个问题。

1. 余弦窗

   如果不加余弦窗，除了那个最原始样本，其他循环移位生成的样本的边缘都比较突兀，也就说这些样本数据是比较差的，会干扰训练的结果。而如果加了余弦窗。 上面是没加余弦窗的情况。除了那个最原始样本，其他样本都是合成的，如果不加余弦窗，那么这些合成样本就会降低分类器的判别能力（如上面c图所示，16张样本中只有两张比较合理）。如果加了余弦窗，就使得图像边缘像素值就都接近于或者等于0，因此循环移位过程中只要目标保持完整那这个样本就是合理的，只有当目标中心接近边缘时，目标跨越边界的那些样本才是错误的，这样以来虽不真实但合理的样本数量就可以增加到大约2/3。

2. regression target y

   这个y是高斯加权后的值。初始目标的位置在padding后的search window的中心，循环移位得到的多个样本反应的是背景信息，而且离中心越远，就越不是目标，所以我们对标签进行高斯加权就刚好可以体现这种可能性准则。KCF里的输出是一个二维response矩阵，里面元素的大小代表该位置下的目标为预测目标的可能性，因此，在训练的时候就是输入是特征，而输出是一个gaussian_shaped_label，一般分类的标签是二值的，或者多值离散的，但是这个高斯标签反应的是由初始目标移位采样形成的若干样本距离初识样本越近可能性越大的准则，在代码中，高斯的峰值被移动到了左上角（于是四个角的值偏大），原因在论文的附录中进行了解释：“after computing a cross-correlation between two images in the Fourier domain and converting back to the spatial domain, it is the top-left element of the result that corresponds to a shift of zero”，也就是说目标零位移对应的是左上角的值。这样一来，我们在预测目标位置的时候，只需要pos=pos+find(response==max(response(:)))就好。如果把峰值放在中心点的话，就会“unnecessarily cause the detection output to be shifted by half a window”。

   补充：在代码中对目标进行padding是为了能让样本中含有特别需要学习的背景信息，而且可以尽量保证样本中目标的完整性，这是考虑循环移位将目标打散了。另外有关高斯加权，可以看一下我的文章computer-vision笔记：图像金字塔与高斯滤波器。

---

效果

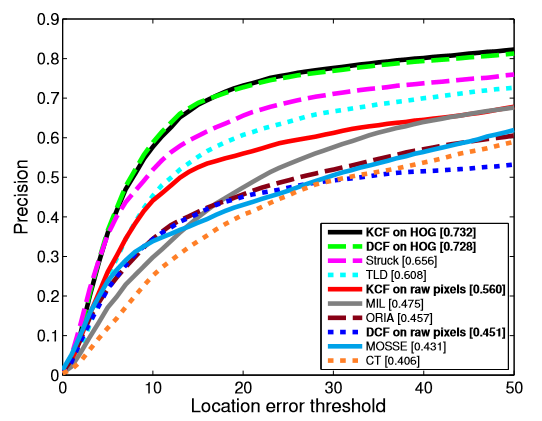
这是KCF在OTB2013上面做的一个实验，由于当时效果比较好的是struck（所以逃不了被针对的命运）。可以看到，KCF（使用HOG特征+高斯核函数）和DCF（也是同一个作者同一篇论文提出的，使用HOG特征+线性核函数，称为对偶相关滤波器）相比于struck来说，精度取得了显著的提升，从0.656提升到了0.732/0.728。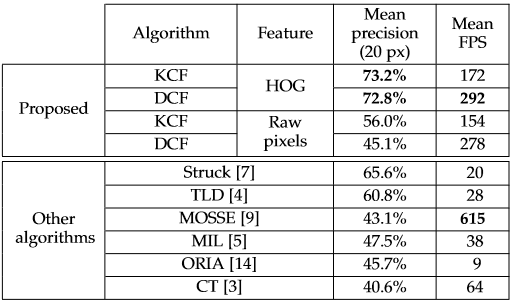

我们还可以根据这个统计图来看一下速度，即使使用了HOG特征和高斯核，KCF的速度还能达到172帧每秒。
此外，用了多通道扩展的DCF取得了更快的速度，但就精度而言较KCF稍差，但也是质的飞跃了。
相较而言，即使用了非常朴素的raw pixels，尽管效果比HOG特征差好多，但是速度并没有提高。这里也证明了HOG特征的强大。
另外可以看到KCF的祖宗MOSSE速度非常亮眼，但这是因为MOSSE它只用了简单的灰度特征，而不是HOG这样高维的特征，可想而知精确度总体效果还是要差一大截的。

---

缺点

1. 缺点一

   对尺度变化的适应性不强。解决办法是加一个尺度变化的比例系数进行多次检测，代价是牺牲一些速度。

2. 缺点二

   对目标快速变形（假设用的是HOG特征）或颜色快速变化（假设用的是颜色特征）不鲁棒。毕竟相关滤波是一种模板类的方法。HOG描述的就是形状信息，形状变化得太快必然会导致效果变差。而如果快速变色，那基于颜色特征的模板肯定也就跟不上了。这个还和模型更新策略与更新速度有关。若采用固定学习率的线性加权更新，那么如果学习率太大，部分或短暂遮挡和任何检测不准确，模型就会学习到背景信息，积累到一定程度模型被背景带飞了；如果学习率太小，目标已经变形了而模板还是那个模板，就会不认识目标，也会降低效果。

3. 缺点三

   对物体快速运动或者低帧率视频不太鲁棒。这两种情况都是意味着在跟踪过程中下一帧图像中目标的位置偏离search window中心太远（要么靠近边缘，要么出去一半，要么全出去）。由于我们是给样本加了余弦窗的，也就是说目标位置靠近边缘会由于余弦窗的存在损失了部分目标信息（变成0），更不用说那些目标超出search window一半或者全超出去的情况了，这也就是CF类算法中的边界效应（Boundary Effects）。

---

其他

头一回看这么“理论”的论文我真的头都大了，要全部搞懂的话估计要花整整一天还不够。真的不得不佩服科研工作者们的智慧，我还是老老实实打基础吧。

原文的理论性、数学性更强，本文把主要的几个核心公式整理了一下，有些许修改和添加，如有疏漏还请多多指教。