computer vision笔记：IoU与GIoU

之前在computer-vision笔记：non-max-suppression中已经介绍过IoU。而在2019年又提出了一种新的损失函数计算方式——GIoU，这里就简述一下其motivation和方法。

References：

电子文献：
https://zhuanlan.zhihu.com/p/94799295

---

IoU的问题

1. IoU与常用的边界框回归损失（smoothL1、均方误差MSE）没有强相关性，即损失相同时，IoU可能会有很大不同。
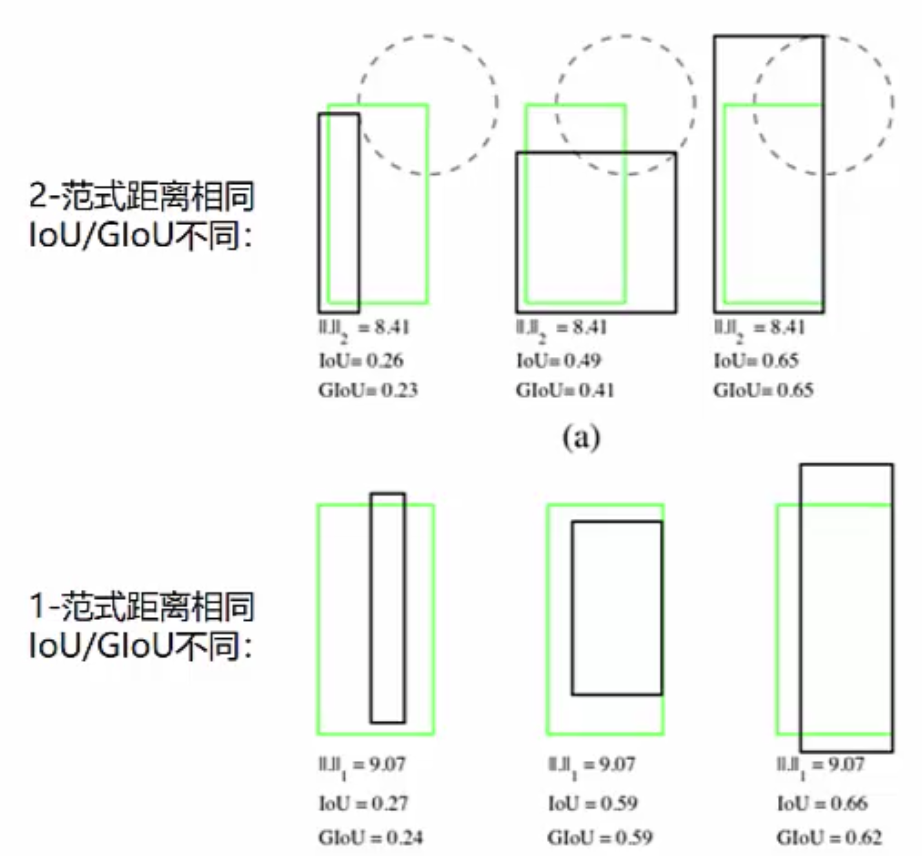
2. 如果两个对象不重叠，则IoU值将为零，可此时就无法反映两个边界框彼此之间的距离。如下图所示，绿框与红框、绿框与蓝框的IoU都是零，可显然蓝框与红框的距离是比绿框要大得多的，这里用IoU就无法体现。
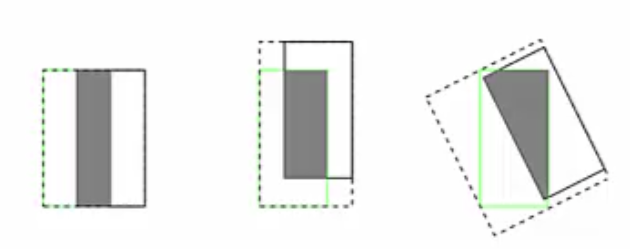
3. IoU还有一个问题就是它无法正确区分两个对象的对齐方式，如下图所示，虽然它们的IoU是相同的，可是对齐方式大不相同，这点IoU也无法体现。

---

GIoU

针对IoU上述问题，GIoU巧妙地改进了定义的方法，提出了一种更强大的方式。简单来说可分为如下三步：

1. 寻找两个边界框的最小闭包区域

   如下图所示，寻找A、B两个边界框的最小闭包区域C，一般就是最小外接凸多边形或者圆形。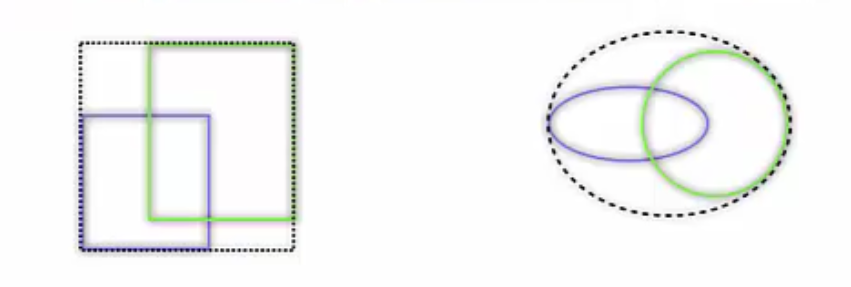

2. 计算IoU

   还是用相同的方法，现计算得出IoU。

3. 计算GIoU

   我们可用如下公式计算GIoU的值 $$GIoU=IoU-\frac{\left | C-(A\bigcup B) \right |}{\left | C \right |}$$ 用文字来描述，即先计算两个框的最小闭包区域面积，再计算闭包区域中不属于两个框的区域占闭包区域的比重，最后用IoU减去这个比重就得到GIoU。
   类似IoU的损失函数$L_{IoU}=1-IoU$，GIoU的损失函数计算公式如下 $$L_{GIoU}=1-GIoU$$

---

效果

实验表明，只需要将边界回归分支的损失修改为GIoU Loss，检测性能可以提升2%-14%，可以说非常引人瞩目了。
在文首给出的参考链接中，也介绍了一种名为DIoU的改进方式，使收敛更加快速，回归更加稳定，这里就不做介绍了。