deep learning笔记：着眼于深度——VGG简介与pytorch实现

发表于 | 更新于: | 分类于 | | 阅读次数:
字数统计: 4.6k字 | 阅读时长 ≈ 19分钟

VGG是我第一个自己编程实践的卷积神经网络，也是挺高兴的，下面我就对VGG在这篇文章中做一个分享。

References：

电子文献：
https://blog.csdn.net/xiaohuihui1994/article/details/89207534
https://blog.csdn.net/sinat_33487968/article/details/83584289
https://blog.csdn.net/qq_32172681/article/details/95971492

参考文献：
[1]Very Deep Convolutional Networks For Large-scale Image Recognition

简介

VGG模型在2014年取得了ILSVRC竞赛的第二名，第一名是GoogLeNet。但是VGG在多个迁移学习任务中的表现要优于GoogleNet。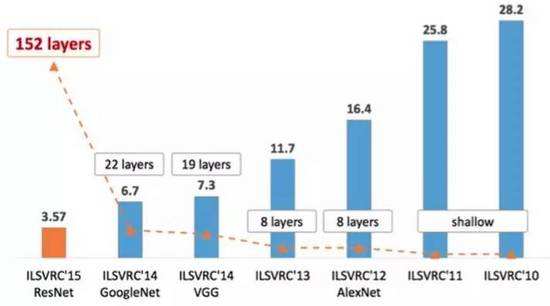

相比之前的神经网络，VGG主要有两大进步：其一是它增加了深度，其二是它使用了小的3x3的卷积核，这可以使它在增加深度的时候一定程度上防止了参数的增长。缺点是它的参数量比较庞大，但这并不意味着它不值得我们仔细研究。下图展示的是VGG的结构。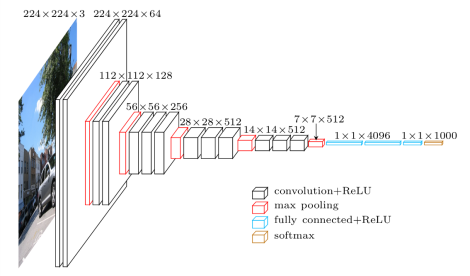

为了通过对比来对VGG的一些改进进行解释，VGG的作者在论文中提供了多个版本。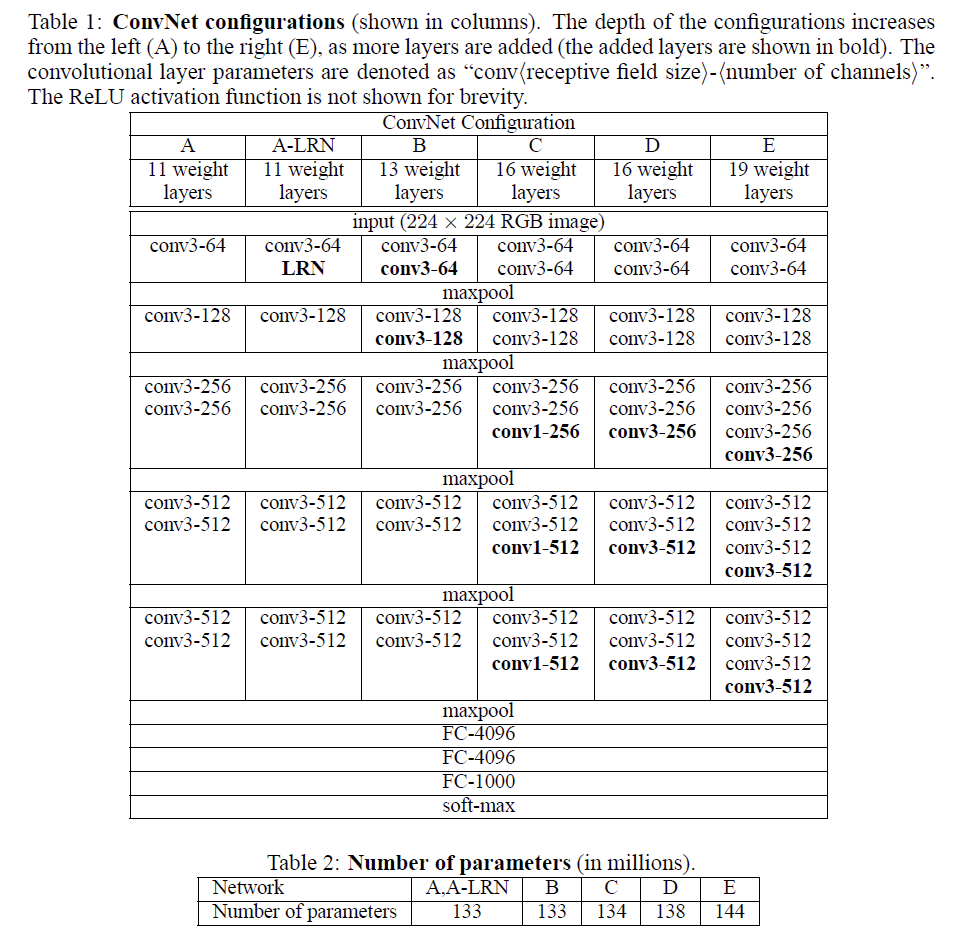

论文

要详细分析VGG，我可能不能像网上写的那样好，更不可能像论文一样明白。那么我在这里就先附上论文。
论文原版
论文中文版
我在英文原版中用黄颜色高亮了我觉得比较重要的内容，大家可以参考一下。
大家也可以自己到网上进行搜索，这类经典的网络网上有许多介绍与分析。
通过论文或者网上的资源对这个网络有一定理解之后，你可以看看我下面的代码实现。

结论

此篇论文的得出了一些结论，总结如下：

  1. 在一定范围内，通过增加网络深度能有效地提升网络性能。这在ResNet里更是得到了显著地体现，上面的ILSVRC历年winner表现统计图就是一个很好的证明，可参见deep-learning笔记：使网络能够更深——ResNet简介与pytorch实现。
  2. 与AlexNet对比可知，多个小卷积核比单个大卷积核性能要好。
  3. AlexNet中用到的LRN层（局部响应归一化层）并没有带来性能的提升，因此可以排除。
  4. 尺度抖动（scale jittering）即多尺度训练、多尺度测试有利于网络性能的提升。
  5. 最佳模型为VGG16，其从头到尾只用了3x3的卷积和2x2的池化。

特点

VGG的特点（创新点）主要有如下四个：

  1. 小卷积核

    VGG使用多个小卷积核来代替大的，这样一方面可以减少参数，另一方面相当于进行了更多的非线性映射，可以增加网络的拟合、表达能力。

  2. 小池化核

    相比AlexNet的3x3池化核，VGG一律采用了2x2的池化核。

  3. 层数更深

    若仅计算conv、fc层的话，VGG中常用的网络层数达到了16、19层（VGG16效果最好），这相较于前几年的研究是一个深度的提升。

  4. conv替代fc

    在基本的CNN中，全连接层的作用是将经过多个卷积层和池化层的图像特征图中的特征进行整合，获取图像特征具有的高层含义，用于图像分类。
    如果我们把全连接层的输出不再看成n个节点的集合，而是视作一个1x1xn的输出层，那么我们就可以用卷积层来替换全连接层了。并且从数学角度看，它和全连接层是一样的。
    因为卷积层没有全连接层对输入的限制，因此使用卷积层代替全连接层可以接收任意宽或高的输入。
    此外，相对于全连接层而言，使用卷积层不会破坏图像的空间结构。这也是一些的网络使用1x1的全卷积层代替全连接层的重要原因。

感受野

这里会涉及一个名为感受野（Receptive Field）的概念，它指的是卷积神经网络每一层输出的特征图（feature map）上的像素点在输入图片上映射的区域大小。简而言之，就是特征图上的一点跟原有图上有关系的点的区域。一般取一个pixel为单位，而输入的感受野就是1即只对应其自身的那个像素。画图易知，两层3x3的卷积层所得到的感受野与一层5x5的卷积层的感受野相同，这也是VGG使用3x3小卷积核来代替的原理之一。
感受野是CNN中一个比较重要的概念，一些目标检测的流行算法如SSD、Faster Rcnn等中的prior box和anchor box的设计都是以感受野为依据的。可以看一下computer-vision笔记：anchor-box。

1x1卷积核

虽然VGG所用的是2x2的卷积核，但是在上文提到了一些网络使用1x1的全卷积层代替全连接层，那么顺便就对1x1卷积核的作用做一个总结。

  1. 如上文所述，使用卷积层就没有全连接层对输入尺寸的限制，这也方便了许多。
  2. 全连接层会改变网络的空间结构，卷积层不会破坏图像的空间结构。一般要学习是相邻的边界等特征，而全连接毫无目的地将整张图“全连接”，换言之全连接输出的是一维向量，势必将丢失大量二维信息，这显然是不合适的。
  3. 可以用于为决策增加非线性因素。
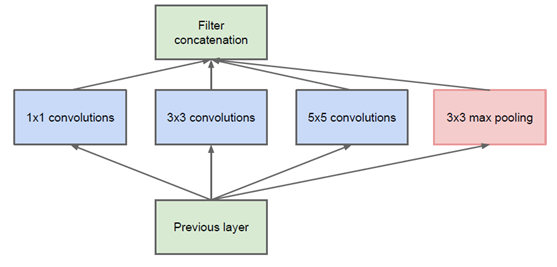
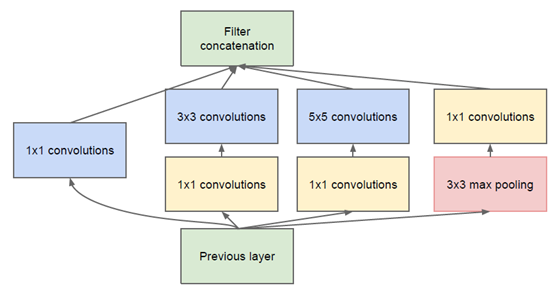
  4. 一些模型用1x1的全连接层来调整网络维度。比如MobileNet使用1x1的卷积核来扩维，GoogleNet、ResNet使用1x1的卷积核来降维。这里的降维类似于压缩处理，并不会影响训练结果，而1x1的卷积核可以使网络变薄，可以成倍地减少计算量。如下图所示，如果我们使用naive的inception，那么最后concatenate出来的特征图厚度会很大，而添加上1x1的卷积核之后就可以调整厚度了。

自己实现

这里我使用pytorch框架来实现VGG。pytorch是一个相对较新的框架，但热度上升很快。根据网上的介绍，pytorch是一个非常适合于学习与科研的深度学习框架。我尝试了之后，也发现上手很快。
在pytorch中，神经网络可以通过torch.nn包来构建。这里我不一一介绍了，大家可以参考pytorch官方中文教程来学习，照着文档自己动手敲一遍之后，基本上就知道了pytorch如何使用了。
为了方便直观的理解，我先提供一个VGG16版本的流程图。

下面是我实现VGG19版本的代码：
首先，我们import所需的包。

1
2
import torch
import torch.nn as nn

接下来，我们定义神经网络。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
class VGG(nn.Module):
    def __init__(self, num_classes = 1000): #imagenet图像库总共1000个类
        super(VGG, self).__init__() #先运行父类nn.Module初始化函数
        
        self.conv1_1 = nn.Conv2d(in_channels = 3, out_channels = 64, kernel_size = 3, padding = 1)
        #定义图像卷积函数：输入为图像（3个频道，即RGB图），输出为64张特征图，卷积核为3x3正方形，为保留原空间分辨率，卷积层的空间填充为1即padding等于1，也就是防止每次卷积尺寸缩小过快导致无法使用更多的卷积层
        self.conv1_2 = nn.Conv2d(in_channels = 64, out_channels = 64, kernel_size = 3, padding = 1)
        
        self.conv2_1 = nn.Conv2d(in_channels = 64, out_channels = 128, kernel_size = 3, padding = 1)
        self.conv2_2 = nn.Conv2d(in_channels = 128, out_channels = 128, kernel_size = 3, padding = 1)
        
        self.conv3_1 = nn.Conv2d(in_channels = 128, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv3_2 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv3_3 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv3_4 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        
        self.conv4_1 = nn.Conv2d(in_channels = 256, out_channels = 512, kernel_size = 3, padding = 1)
        self.conv4_2 = nn.Conv2d(in_channels = 512, out_channels = 512, kernel_size = 3, padding = 1)
        self.conv4_3 = nn.Conv2d(in_channels = 512, out_channels = 512, kernel_size = 3, padding = 1)
        self.conv4_4 = nn.Conv2d(in_channels = 512, out_channels = 512, kernel_size = 3, padding = 1)
        
        self.conv5_1 = nn.Conv2d(in_channels = 512, out_channels = 512, kernel_size = 3, padding = 1)
        self.conv5_2 = nn.Conv2d(in_channels = 512, out_channels = 512, kernel_size = 3, padding = 1)
        self.conv5_3 = nn.Conv2d(in_channels = 512, out_channels = 512, kernel_size = 3, padding = 1)
        self.conv5_4 = nn.Conv2d(in_channels = 512, out_channels = 512, kernel_size = 3, padding = 1)
        
        self.relu = nn.ReLU(inplace = True) #inplace=TRUE表示原地操作
        self.max = nn.MaxPool2d(kernel_size = 2, stride = 2)
        
        self.fc1 = nn.Linear(512 * 7 * 7, 4096) #定义全连接函数1为线性函数:y = Wx + b，并将512*7*7个节点连接到4096个节点上
        self.fc2 = nn.Linear(4096, 4096)
        self.fc3 = nn.Linear(4096, num_classes)
        #定义全连接函数3为线性函数:y = Wx + b，并将4096个节点连接到num_classes个节点上，然后可用softmax进行处理
        
        #定义该神经网络的向前传播函数，该函数必须定义，一旦定义成功，向后传播函数也会自动生成（autograd）
    def forward(self, x):
        
        x = self.relu(self.conv1_1(x))
        x = self.relu(self.conv1_2(x))
        x = self.max(x) 
        #输入x经过卷积之后，经过激活函数ReLU，循环两次，最后使用2x2的窗口进行最大池化Max pooling，然后更新到x
        
        x = self.relu(self.conv2_1(x))
        x = self.relu(self.conv2_2(x))
        x = self.max(x)
        
        x = self.relu(self.conv3_1(x))
        x = self.relu(self.conv3_2(x))
        x = self.relu(self.conv3_3(x))
        x = self.relu(self.conv3_4(x))
        x = self.max(x)
        
        x = self.relu(self.conv4_1(x))
        x = self.relu(self.conv4_2(x))
        x = self.relu(self.conv4_3(x))
        x = self.relu(self.conv4_4(x))
        x = self.max(x)
        
        x = self.relu(self.conv5_1(x))
        x = self.relu(self.conv5_2(x))
        x = self.relu(self.conv5_3(x))
        x = self.relu(self.conv5_4(x))
        x = self.max(x)
        
        x = x.view(-1, self.num_flat_features(x)) #view函数将张量x变形成一维的向量形式,总特征数并不改变,为接下来的全连接作准备
        
        x = self.fc1(x) #输入x经过全连接1，然后更新x
        x = self.fc2(x)
        x = self.fc3(x)
        return x
    
    def num_flat_features(self, x):
        size = x.size()[1:]  #all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

vgg = VGG()
print(vgg)

我们print网络，可以看到输出如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
VGG(
  (conv1_1): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv1_2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv2_1): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv2_2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv3_1): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv3_2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv3_3): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv3_4): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv4_1): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv4_2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv4_3): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv4_4): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv5_1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv5_2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv5_3): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv5_4): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (relu): ReLU(inplace=True)
  (max): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (fc1): Linear(in_features=25088, out_features=4096, bias=True)
  (fc2): Linear(in_features=4096, out_features=4096, bias=True)
  (fc3): Linear(in_features=4096, out_features=1000, bias=True)
)

最后我们随机生成一个张量来进行验证。

1
2
3
input = torch.randn(1, 3, 224, 224)
out = vgg(input)
print(out)

其中(1, 3, 224, 224)表示1个3x224x224的矩阵，这是因为VGG输入的是固定尺寸的224x224的RGB（三通道）图像。
如果没有报错，那么就说明你的神经网络成功运行通过了。
我们也可以使用torch.nn.functional来实现激活函数与池化层，这样的话，你需要还需要多引入一个包：

1
2
3
import torch
import torch.nn as nn
import torch.nn.functional as F #新增

同时，你不需要在init中实例化激活函数与最大池化层，相应的，你需要对forward前馈函数进行更改：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def forward(self, x):
        
        x = F.relu(self.conv1_1(x))
        x = F.relu(self.conv1_2(x))
        x = F.max_pool2d(x, kernel_size = 2, stride = 2) 
        #输入x经过卷积之后，经过激活函数ReLU，循环两次，最后使用2x2的窗口进行最大池化Max pooling，然后更新到x
        
        x = F.relu(self.conv2_1(x))
        x = F.relu(self.conv2_2(x))
        x = F.max_pool2d(x, kernel_size = 2, stride = 2)
        
        x = F.relu(self.conv3_1(x))
        x = F.relu(self.conv3_2(x))
        x = F.relu(self.conv3_3(x))
        x = F.relu(self.conv3_4(x))
        x = F.max_pool2d(x, kernel_size = 2, stride = 2)
        
        x = F.relu(self.conv4_1(x))
        x = F.relu(self.conv4_2(x))
        x = F.relu(self.conv4_3(x))
        x = F.relu(self.conv4_4(x))
        x = F.max_pool2d(x, kernel_size = 2, stride = 2)
        
        x = F.relu(self.conv5_1(x))
        x = F.relu(self.conv5_2(x))
        x = F.relu(self.conv5_3(x))
        x = F.relu(self.conv5_4(x))
        x = F.max_pool2d(x, kernel_size = 2, stride = 2)
        
        x = x.view(-1, self.num_flat_features(x)) #view函数将张量x变形成一维的向量形式,总特征数并不改变,为接下来的全连接作准备
        
        x = self.fc1(x) #输入x经过全连接1，然后更新x
        x = self.fc2(x)
        x = self.fc3(x)
        return x

如果你之前运行通过的话，那么这里也是没有问题的。
这里我想说明一下torch.nn与torch.nn.functional的区别。
这两个包中有许多类似的激活函数与损失函数，但是它们又有如下不同：
首先，在定义函数层（继承nn.Module）时，init函数中应该用torch.nn，例如torch.nn.ReLU，torch.nn.Dropout2d，而forward中应该用torch.nn.functional，例如torch.nn.functional.relu，不过请注意，init里面定义的是标准的网络层。只有torch.nn定义的才会进行训练。torch.nn.functional定义的需要自己手动设置参数。所以通常，激活函数或者卷积之类的都用torch.nn定义。
另外，torch.nn是类，必须要先在init中实例化，然后在forward中使用，而torch.nn.functional可以直接在forward中使用。
大家还可以通过官方文档torch.nn.functional与torch.nn来进一步了解两者的区别。
大家或许发现，我的代码中有大量的重复性工作。是的，你将在文章后面的官方实现中看到优化的代码，但是相对来说，我的代码更加直观些，完全是按照网络的结构顺序从上到下编写的，可以方便初学者（including myself）的理解。

出现的问题

虽然我的代码比较简单直白，但是过程中并不是一帆风顺的，出现了两次报错：

  1. 输入输出不匹配

    当我第一遍运行时，出现了一个RuntimeError： 这是一个超级低级的错误，经学长提醒后我才发现，我两个卷积层之间输出输入的channel数并不匹配： 唉又是ctrl+C+V惹的祸，改正后的网络可以参见上文。
    在这里，我想提醒我自己和大家注意一下卷积层输入输出的维度公式：
    假设输入的宽、高记为W、H。
    超参数中，卷积核的维度是F，stride步长是S，padding是P。
    那么输出的宽X与高Y可用如下公式表示：然而，当我在计算ResNet的维度的时候，发现套用这个公式是除不尽的。于是我搜索到了如下规则：
    1. 对卷积层操作，除不尽时，向下取整。
    2. 对池化层操作，除不尽时，向上取整。

  2. 没有把张量转化成一维向量

    上面的问题解决了，结果还有错误：

    根据报错，可以发现3584x7是等于25088的，结合pytorch官方文档，我意识到我在把张量输入全连接层时，没有把它拍扁成一维。因此，我按照官方文档添加了如下代码：

    1
    2
    3
    4
    5
    6
    7
    8
    x = x.view(-1, self.num_flat_features(x))

    def num_flat_features(self, x):
        size = x.size()[1:]  #all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

    再运行，问题解决。
    注意这里的“except the batch dimension”，我在后面deep-learning笔记：记首次ResNet实战中就踩了坑。

另外，我原本写的代码中，在卷积层之间的对应位置都加上了relu激活函数与池化层。后来我才意识到，由于它们不具有任何需要学习的参数，我可以直接把它们拿出来单独定义：

1
2
self.relu = nn.ReLU(inplace = True)
self.max = nn.MaxPool2d(kernel_size = 2, stride = 2)

虽然是一些很低级的坑，但我还是想写下来供我自己和大家今后参考。

官方源码

由于VGG的结构设计非常有规律，因此官方源码给出了更简洁的版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import torch.nn as nn
import math

class VGG(nn.Module):

    def __init__(self, features, num_classes=1000, init_weights=True):
        super(VGG, self).__init__()
        self.features = features
        self.classifier = nn.Sequential(
            nn.Linear(512 * 7 * 7, 4096),
            nn.ReLU(True),
            nn.Dropout(),
            nn.Linear(4096, 4096),
            nn.ReLU(True),
            nn.Dropout(),
            nn.Linear(4096, num_classes),
        )
        if init_weights:
            self._initialize_weights()

    def forward(self, x):
        x = self.features(x)
        x = x.view(x.size(0), -1)
        x = self.classifier(x)
        return x

    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
                m.weight.data.normal_(0, math.sqrt(2. / n))
                if m.bias is not None:
                    m.bias.data.zero_()
            elif isinstance(m, nn.BatchNorm2d):
                m.weight.data.fill_(1)
                m.bias.data.zero_()
            elif isinstance(m, nn.Linear):
                m.weight.data.normal_(0, 0.01)
                m.bias.data.zero_()

因为VGG中卷积层的重复性比较高，所以官方使用一个函数来循环产生卷积层：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def make_layers(cfg, batch_norm=False):
    layers = []
    in_channels = 3
    for v in cfg:
        if v == 'M':
            layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
        else:
            conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)
            if batch_norm:
                layers += [conv2d, nn.BatchNorm2d(v), nn.ReLU(inplace=True)]
            else:
                layers += [conv2d, nn.ReLU(inplace=True)]
            in_channels = v
    return nn.Sequential(*layers)

接下来定义各个版本的卷积层（可参考上文中对论文的截图），这里的“M”表示的是最大池化层。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
cfg = {
    'A': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
    'B': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
    'D': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
    'E': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}

def vgg11(**kwargs):
    model = VGG(make_layers(cfg['A']), **kwargs)
    return model

def vgg11_bn(**kwargs):
    model = VGG(make_layers(cfg['A'], batch_norm=True), **kwargs)
    return model

def vgg13(**kwargs):
    model = VGG(make_layers(cfg['B']), **kwargs)
    return model

def vgg13_bn(**kwargs):
    model = VGG(make_layers(cfg['B'], batch_norm=True), **kwargs)
    return model

def vgg16(**kwargs):
    model = VGG(make_layers(cfg['D']), **kwargs)
    return model

def vgg16_bn(**kwargs):
    model = VGG(make_layers(cfg['D'], batch_norm=True), **kwargs)
    return model

def vgg19(**kwargs):
    model = VGG(make_layers(cfg['E']), **kwargs)
    return model

def vgg19_bn(**kwargs):
    model = VGG(make_layers(cfg['E'], batch_norm=True), **kwargs)
    return model

if __name__ == '__main__':
    # 'VGG', 'vgg11', 'vgg11_bn', 'vgg13', 'vgg13_bn', 'vgg16', 'vgg16_bn', 'vgg19_bn', 'vgg19'
    # Example
    net11 = vgg11()
    print(net11)

附上pytorch官方源码链接。可以在vision/torchvision/models/下找到一系列用pytorch实现的经典神经网络模型。
好了，以上就是VGG的介绍与实现，如有不足之处欢迎大家补充！

碰到底线咯 后面没有啦

本文标题:deep learning笔记：着眼于深度——VGG简介与pytorch实现

文章作者:高深远

发布时间:2019年09月15日 - 07:38

最后更新:2020年02月15日 - 22:10

原始链接:https://gsy00517.github.io/deep-learning20190915073809/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

0%