元学习（Meta Learning）即让机器学习如何去学习（learn to learn）。我前几天看到这个概念，觉得非常有意思，这几天也一直在看相关的概念和implement，发现其实很多方法或者思想已经在最新的一些工作中得到有意或者无意运用。因此我决定对我目前的了解做一个总结，或许能给之后的思考带来启发。
强烈推荐台湾教授李宏毅关于Meta Learning的课程录像，油管上有资源，总共4个part，讲得真的非常清楚！
此外，斯坦福在2019年秋季也推出了多任务学习和元学习的CS330，感兴趣可以看一看，语速稍快，可以锻炼一下英语。
由于目前对这个领域的了解还不够深入，分类可能不是很恰当，以后待理解加深之后再做调整，如有错误还请见谅。
References：
电子文献：
https://cloud.tencent.com/developer/article/1463397
https://zhuanlan.zhihu.com/p/28639662
https://mp.weixin.qq.com/s/MApZS0-SL4FNP2kmavhcxQ
https://blog.csdn.net/liuglen/article/details/84770069
https://blog.csdn.net/mao_feng/article/details/78939864
https://blog.csdn.net/ppp8300885/article/details/80383246
元学习
人工智能的一个基本问题是它无法像人类一样高效地学习。
与人类相比，大多数最先进的深度学习方法都有两个关键的弱点：
样本效率低
深度学习的样本效率很差，学习效率很低下。尽管目前已经有许多深度学习模型显示了超人的表现，但达到这种效果需要数百万个训练样本来训练。也就是说对one-shot learning和few-shot learning的能力还是不够强。可移植性差
许多模型不会从以前的经验或学到的知识中学习。也就是说训练得到的知识是不共享的，并且每个任务都独立于其他任务进行训练。
基于以上这些问题的考虑，“元学习”被提出，它研究的不是如何提升模型解决某项具体的任务（分类、回归、检测）的能力，而是研究如何提升模型解决一系列任务的能力。它是增强学习之后的一个研究分支，总的来看，人工智能的研究呈现出了从Artificial Intelligence，到Machine Learning，到Deep Learning，到Deep Reinforcement Learning，再到Deep Meta Learning这样一个大体的方向，这样下去或许最后就真的能够创造出自己学习的机器了。也就是说：
在过去，我们不仅知道机器是怎么想的，而且知道机器是怎么学的。
目前，我们虽然不知道机器是怎么想的，但是知道机器是怎么学的。
未来，我们非但不知道机器是怎么想的，还不知道机器是怎么学的。
也就是从人工智能到智能。
哈哈上面扯远了，前面说过，我们可以将元学习定义为“学习如何学习”。但是实际上，我们还不知道确切的定义或解决方案。因此，它仍然是一个宽松的术语，指的是不同的方法。比如，从某种意义上来说，我们可以认为迁移学习也是一种元学习。它利用别的任务中训练得比较好的参数，使得在本任务得数据集上能够更好更快地达到最优。
一般可以将Meta Learning分成两个阶段：
Gradual Learning
也就是通过在一些相似任务上训练得到Meta Learner，它具有较强的泛化能力。Rapid Learning
也就是利用该Meta Learner直到之后的学习过程，使模型能够快速调整以适应新的任务。
在李宏毅的课程中提到，Machine Learning其实就是学习如何根据数据找出一个$f$函数，使得在测试中，该函数能根据输入获得正确的输出。而Meta Learning其实就是找到一个$F$函数，这个$F$函数的能力是找出$f$函数，也就是说，不同于机器学习直接找$f$，元学习中机器的任务是去找这个$F$。
来看下图，这里说的其实就是一个训练的过程，通过训练找出最终模型中效果最好的参数$\widehat{\theta }$。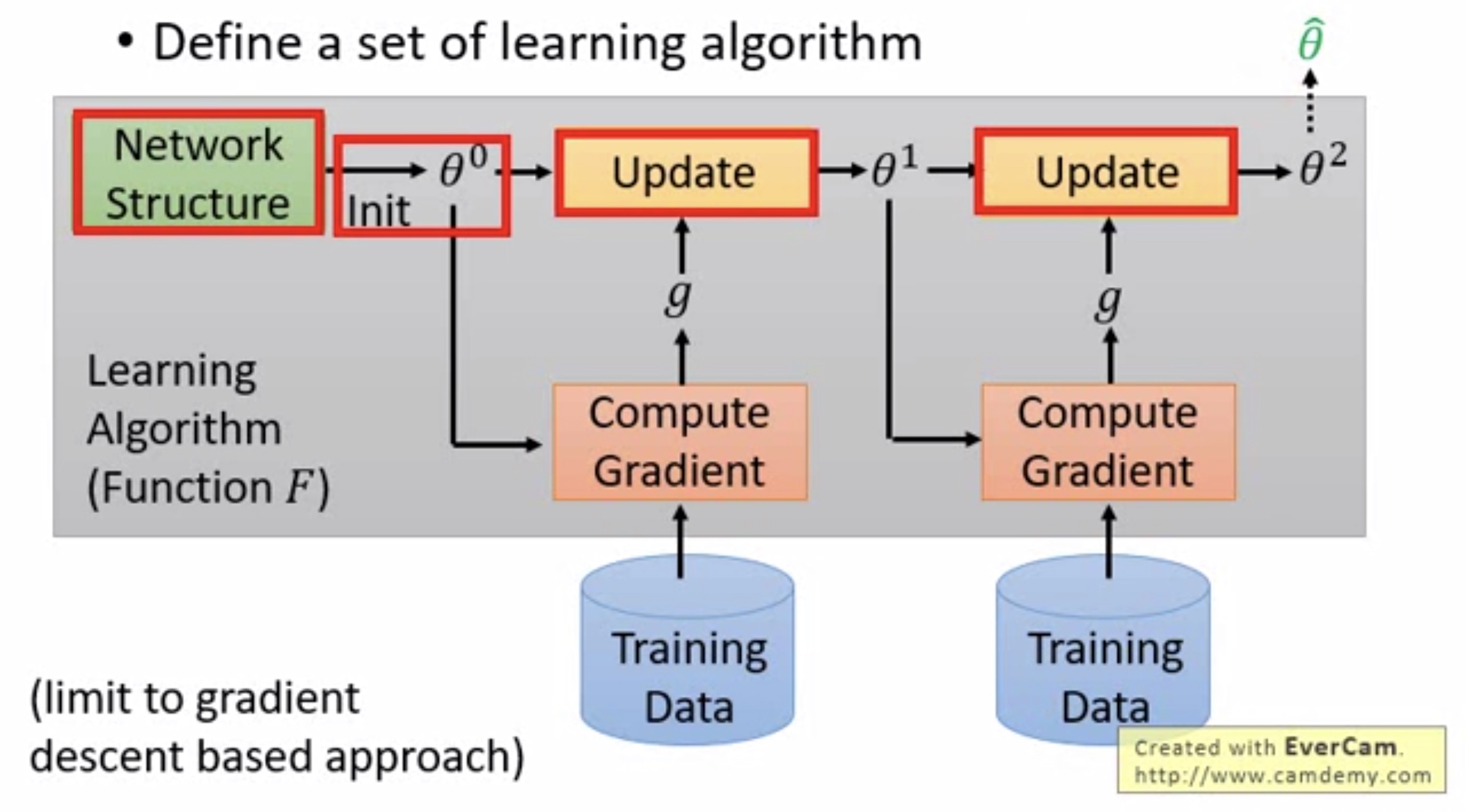
可以看上图红框圈出的部分，仔细想想，这些部分的不同也就构成了不同的算法。然而，目前这些红框中的结构基本上还是人为设计定义的。那么元学习思考的就是能不能让机器自己学习其中的方法与结构。
数据集划分
由于元学习学习的是解决一系列任务的能力，因此不同于以往的将数据集划分成训练集和测试集（或许还有验证集），在元学习中，我们将数据集分割成Training Tasks、Testing Tasks（、Validaiton Tasks）。每一个任务都包含一个训练集和一个测试集。为了区别，这里称这些小训练集为Support Set，称这些小测试集为Query Set。
元学习与one-shot learning
一般来说，元学习总是与one-shot learning相结合的。我们知道，目前许多单任务模型的训练都是以天计数的。而元学习的训练集中每一组数据都是一个任务，假如Training Tasks中有n个任务，那就是说我们要训练n次也就是单任务模型的训练时间的n倍，这也意味着我们需要很长的时间才能检验一次效果，显然是不划算的。
而one-shot learning虽然只提供了少量的数据，但这也是它的一个优势——训练更快，因此我们对one-shot learning任务进行元学习，可以在较短的时间内看到训练效果。
学习初值的元学习
上文说过可以让机器自己学习红框中的结构与方法，这里有元学习中两种代表性的方法MAML和Reptile，它们都学习的是初始化的方式（上图第二个红框）。MAML音同mammal（哺乳动物），也是Model Agnostic Meta Learning的缩写；而Reptile（意为爬行动物），由于找不到缩写的来源，严重怀疑是故意这么命名来与MAML对应。
它们两者实际上学习的是该把初始化参数$\phi $设成什么，其损失函数为
这里的$\widehat{\theta }^{n}$其实就是在第n个任务中，由初始参数$\phi $通过Support Set学到的最终模型中的参数。而$l^{n}\left ( \widehat{\theta }^{n} \right )$就是对于第n个任务在Query Set上的损失。
首先我借用李宏毅老师给的例子来弄明白这里“学习把参数$\phi $初始化成什么”到底与普通的训练中“学习把参数训练成什么”有什么区别。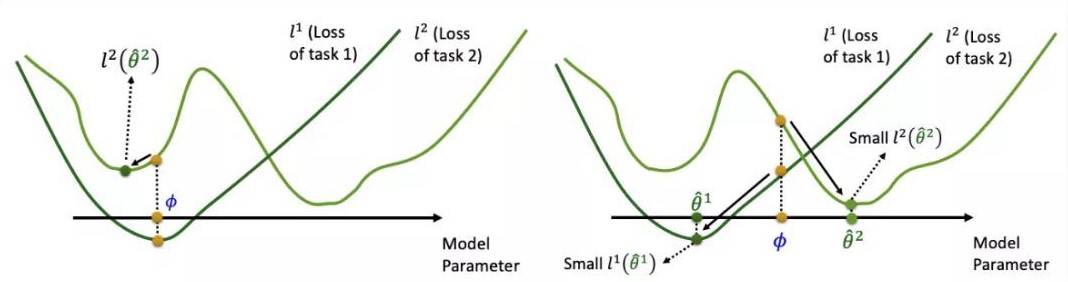
在上图中，左图表示的是我们一般意义上的训练（Model Pre-training），右图表示的是MAML或者Reptile中的初始化。可以看到，左图最终训练得出的参数$\phi $在task 1（Training Tasks）上表现得最好，但在一个不同的任务task 2（Testing Tasks）上，它只能收敛到局部最优点（local minima）。在右图中，虽然在Training Tasks上表现得不是最好，但是在遇到新的任务训练时，现在的初始化参数$\phi $可以很快很好地收敛到全局最优点（global minima）。
也就是说，一般意义上的训练，我们关注的是在所有Training Tasks上达到最好的情况，比如找出让训练时的损失函数最小的一组参数，但我们并不关注拿此时的参数去新任务上进行训练是否会得到好的结果；而在学习初始化的元学习中，我们不在意$\phi $在Training Tasks中表现得有多好，我们在意的是拿初始化后的$\phi $到下一个任务上去训练能够很快很好地取得不错的表现。简而言之，Model Pre-training关注的是$\phi $当前的表现，而Meta Learning关注的是$\phi $未来遇到新任务时的潜力。如果说到这里还不是很清楚，后文还有直观的理解。
具体怎么找到这个$\phi $呢？这就产生了下面两种方法。
MAML模型无关元学习
MAML考虑的是训练出一个初始化参数$\phi $，使得拥有这个参数的模型在遇到一个新的任务时能够一步到位达到最好，比如接收到一张新的图片就可以快速训练成为辨别该图片同一类别图片的最优模型。
当然，寻找这个$\phi $的方法还是梯度下降，因此也要求$\phi $关于损失函数$L$的偏导数。由于MAML考虑的是模型在遇到新任务时一步到位，因此$\widehat{\theta }$也仅进行一次梯度下降，如下所示。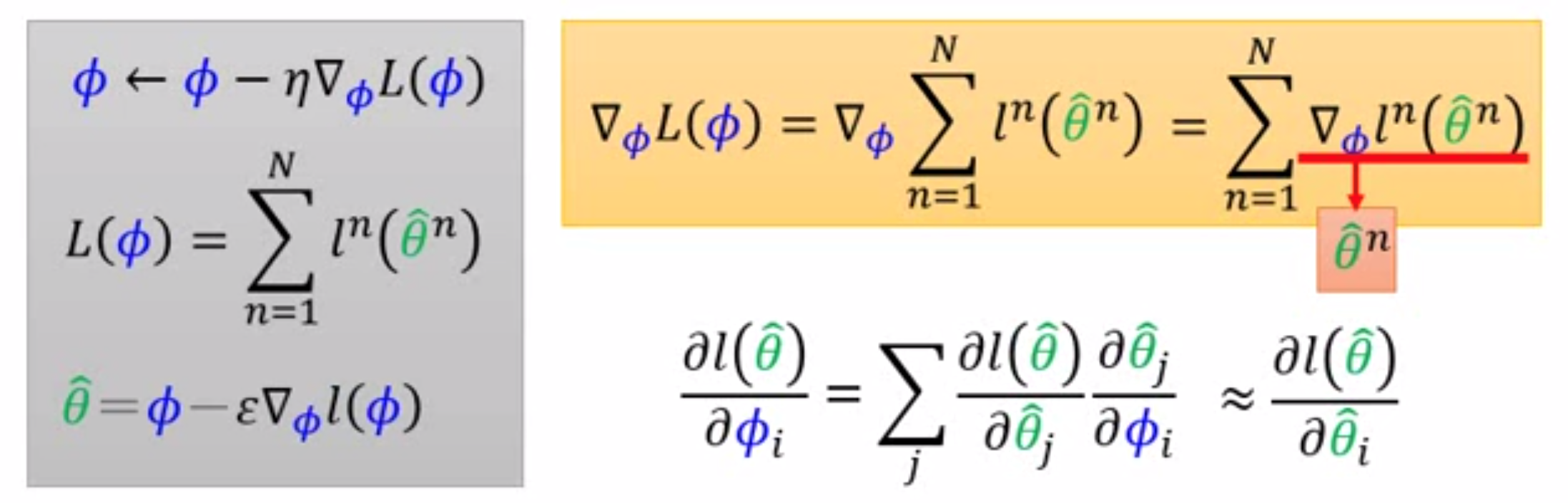
由于这里$\widehat{\theta }_{j}$对$\phi _{i}$的偏导数还是要分类讨论很麻烦，因此作者使用了a first-order approximation，如下图所示。 
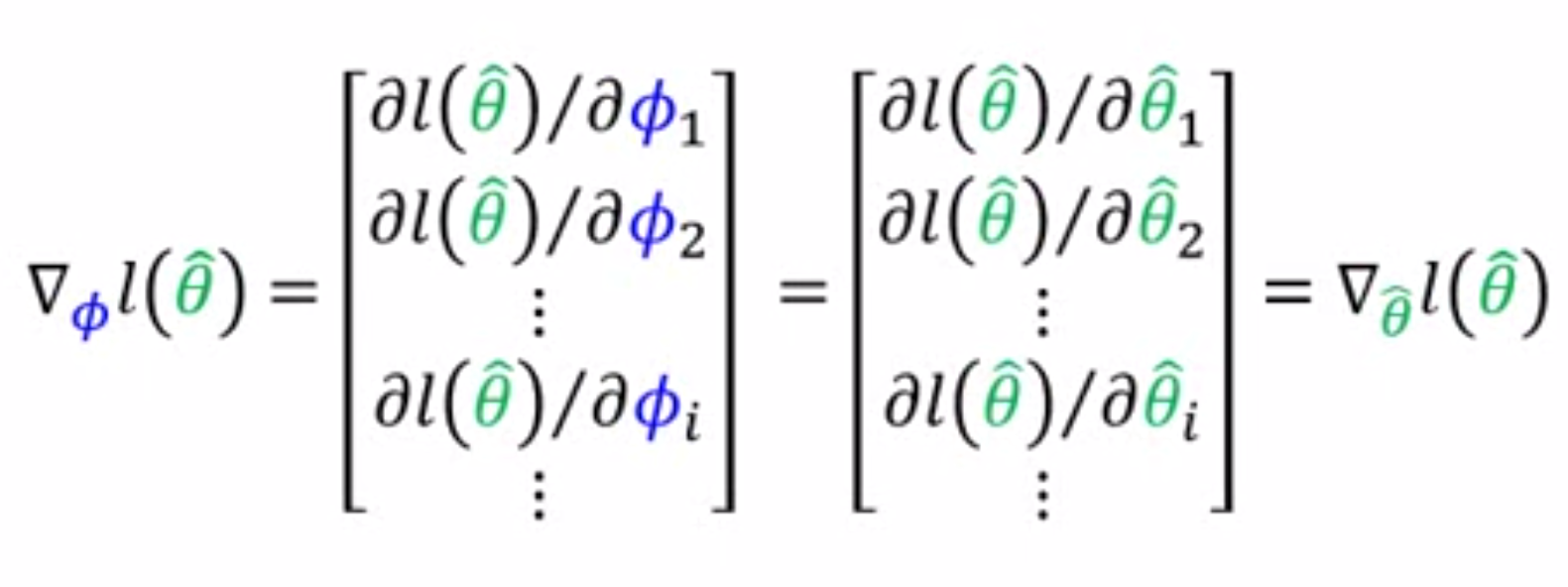也就是当且仅当$i$等于$j$的时候时取$\widehat{\theta }_{j}$对$\phi _{i}$的偏导数为1，否则取偏导数为0。
我们可以来直观地看一下MAML在做什么。如下图所示，左为MAML，右为Model Pre-training，上文已比较过两者关注点的不同，这里再看看两者方法上的不同。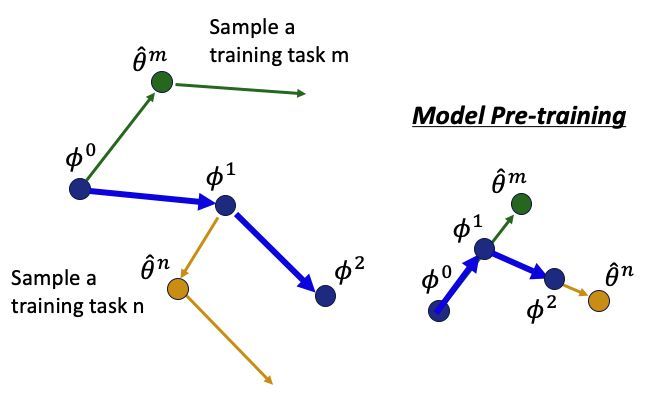
MAML首先在第一个任务采样出来的样本上计算损失函数并进行一次梯度下降，然后用此时的参数计算损失函数再进行一次梯度下降，最后，根据第二次梯度下降的梯度方向，平行地对原参数$\phi $进行一次梯度下降。注意，这里每一次梯度下降使用的学习率不需要一样。可以这样理解，第二次梯度下降后的参数相比第一次梯度下降后的参数在task m上表现要好，因此$\phi $沿相同的方向梯度下降，就能使在遇到task m的时以更少的训练次数到达离较优的第二次梯度下降后的参数更近的位置。在task n上同理。
而Model Pre-training，则是要求在训练的每个任务上尽可能做到最好，于是直接朝着由每个任务采样样本得到的损失函数计算出的梯度的方向靠近。
其实，Model Pre-training的基本思想就是每训练完一个任务，我们就把这过程中的信息用来更新模型。而Meta Learning的基本思想就是找到所有学习任务背后的基础知识。因此，我们不会立即更新模型，而是等待一批任务完成。稍后，我们将从这些任务中学到的所有知识合并到一个更新中。
个人感觉，这有点像想要去做、却为了大局而保持一点克制的感觉，似乎的确蕴含了一点点人生哲理在里面。 
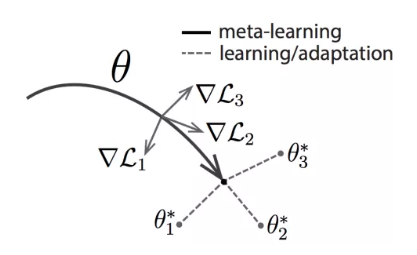
Reptile一阶元学习
Reptile的思想其实是和MAML一样的，只不过它使用了多次梯度下降后的方向来更新$\phi _{i}$，也就是对遇到一个新任务时的更新次数不加限制，不指望一步到位。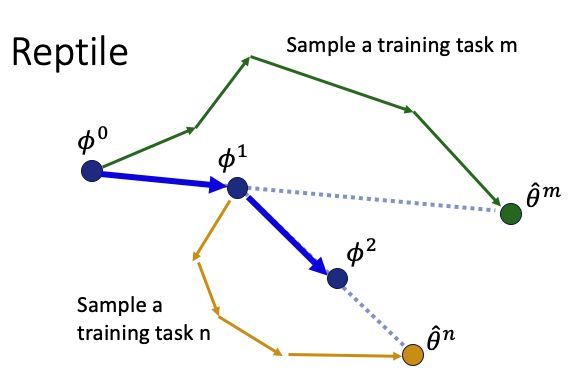
我们可以通过Pre-training、MAML和Reptile的对比图来理解一下Reptile改进的思想，它相当于在当下的任务和未来的任务之间寻找一个平衡。 
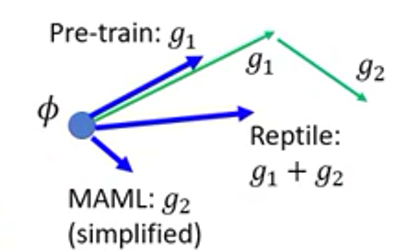我觉得就泛化能力而言，MAML可能还是要好于Reptile的。
实际上，在MAML的使用中，我们也可以进行多次梯度下降，训练时假设一步到位并不意味着在实际使用的时候只能使用一次梯度下降。
李宏毅老师在课程中还给出了一个toy example的例子，区分Model Pre-training和Meta Learning。如下所示，toy example的目标是拟合正弦曲线
这里的$a$和$b$是任取的随机数，也就是每个任务都是拟合一个不同的正弦曲线。
来看看两种方法的训练结果，其中左边是Model Pre-training的结果，右边是Meta Learning的结果，这里使用的是MAML方法。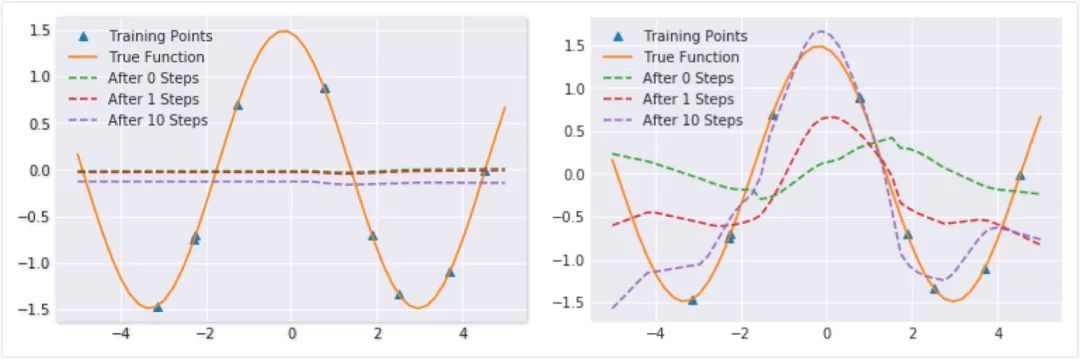
图中绿色的线就是训练好之后的参数构成的模型。可以看到，Model Pre-training为了在训练集中各种正弦曲线中达到损失函数最小，训练结果为一条直线，这在测试时效果很差；而MAML则预备在遇到一个新的曲线时能很快地去拟合，在测试时能很快地达到很好的效果。
然而，目前这类方法的效果好像仅在多样性较低的任务分布中进行实验得到了验证，在这些任务上做得好不代表在复杂程度不同、模式不同的任务上也可以有很好的表现。对于应用在高复杂度的任务上的效果可能还是要打个问号的，在这方面的研究还有很长的路要走。
补充：其实这两种方法后面还是有比较复杂的数学推导的，我在网上看到一个博客写得挺好，补充在这里MAML-模型无关元学习算法、Reptile-一阶元学习算法。
学习更新的学习
上一节介绍的是如何让机器自己学习出一个初始化的方法，前文圈出的红框中另有一项是Update，那么我们是否可以学习如何更新模型呢？
借鉴LSTM
之前没有看过LSTM，所以我想顺便也理一下LSTM的基本思路。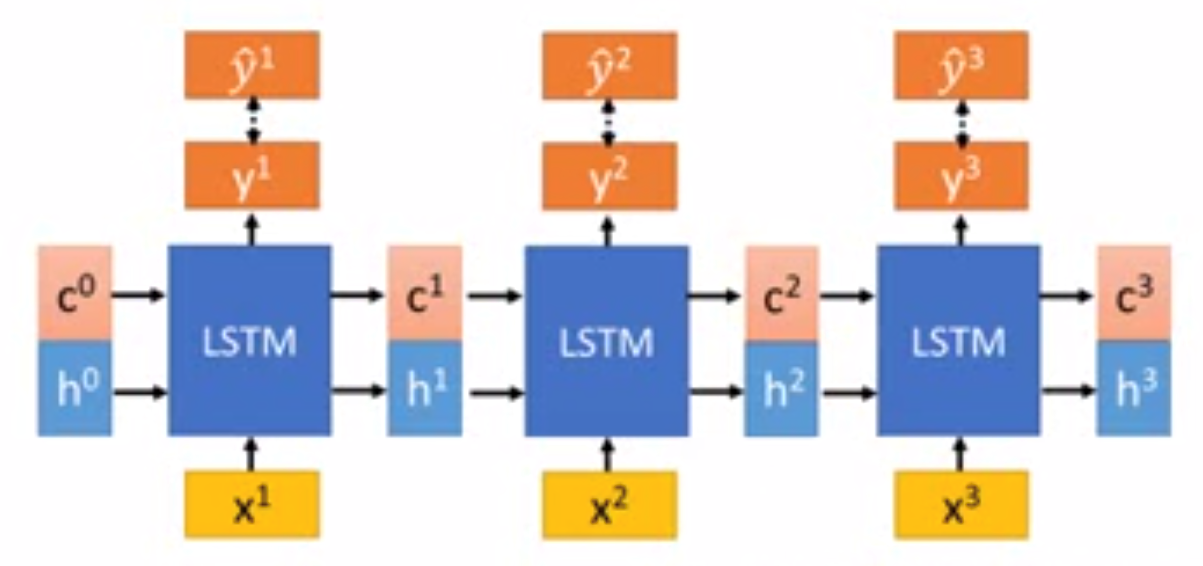
相比于RNN，LSTM从前一级获得的输入有两个（也可以看作将一个输入拆成两段），区别就在于$c$更新得更慢，$h$更新得更快。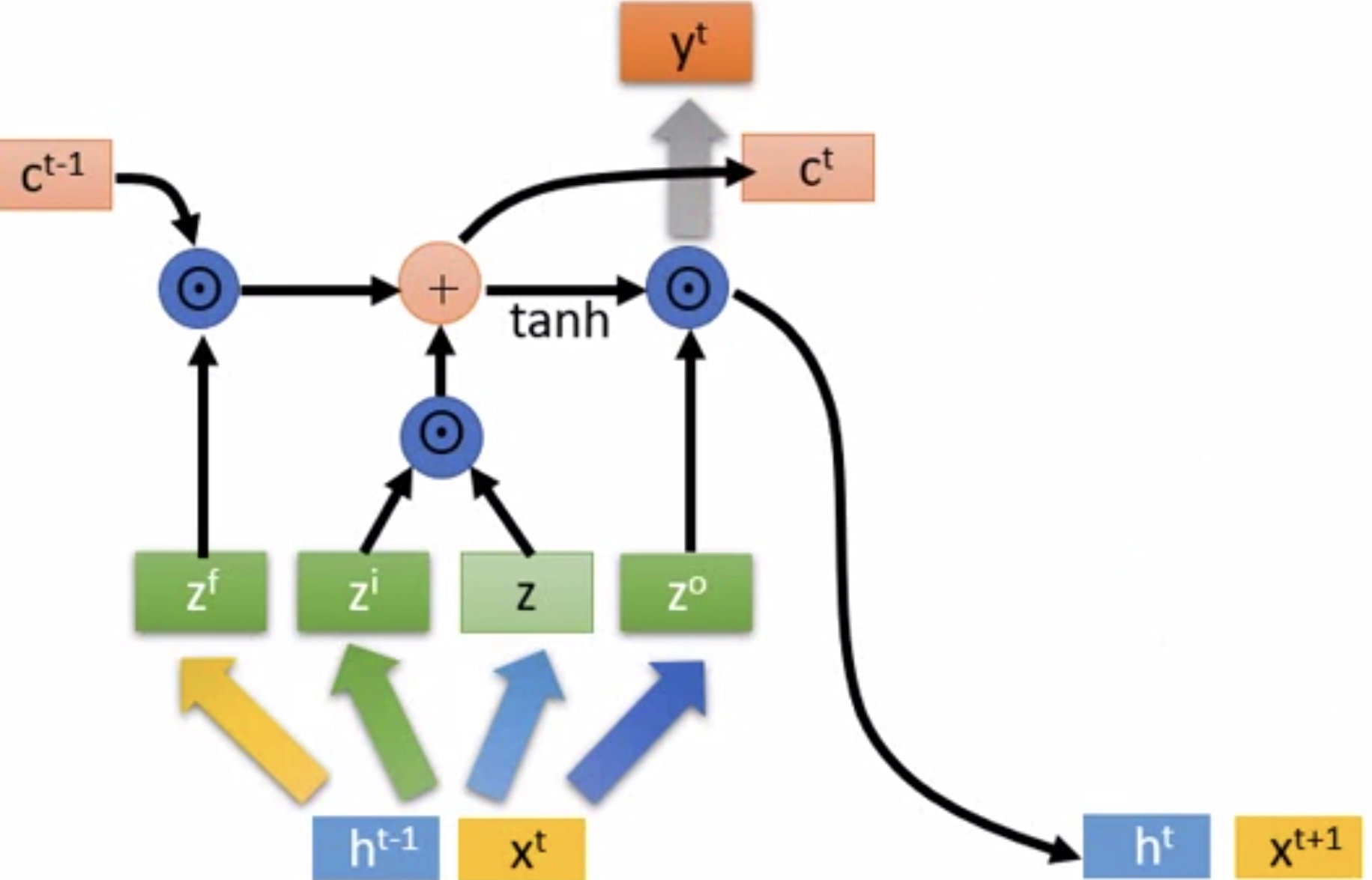
这里各个参数表示的含义如下所示，$\sigma $表示的是某种函数。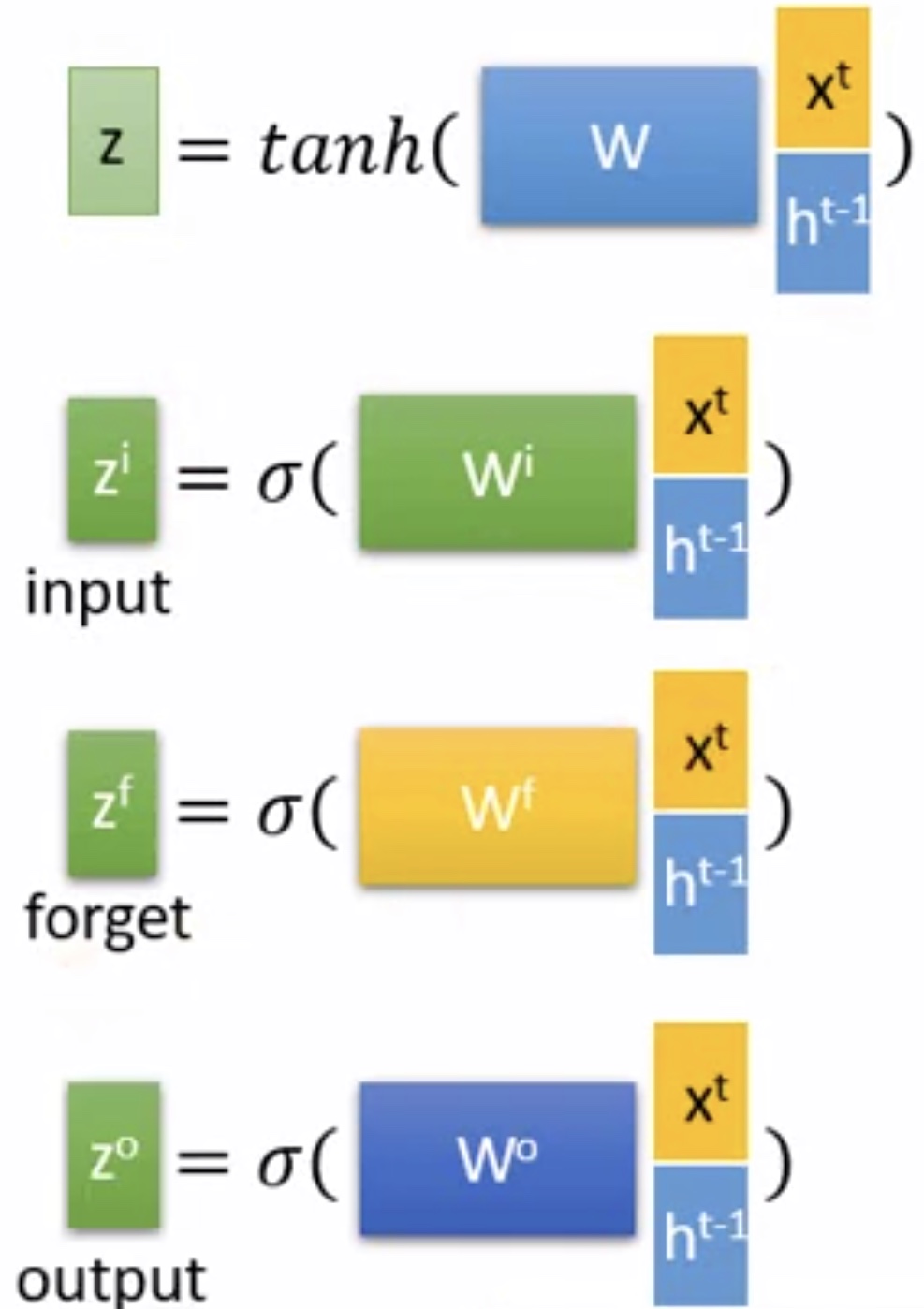
每一块的输出和传递给下一级的$c$与$h$计算方法如下所示，这里表示的是点乘操作。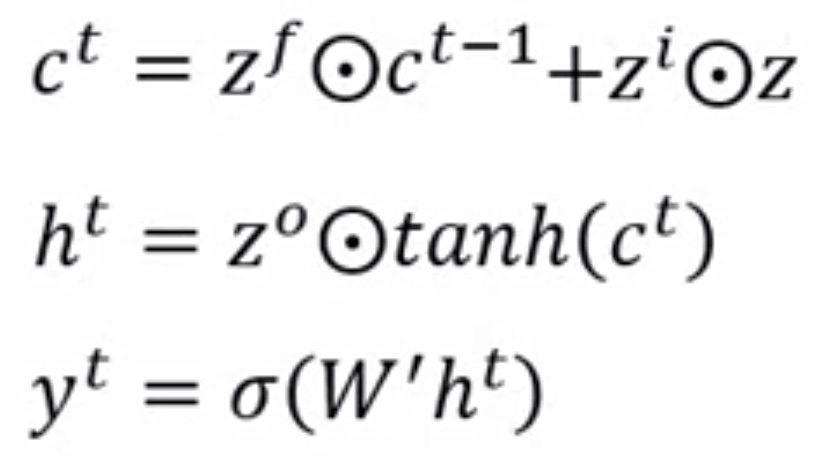
方法1
一般而言，我们梯度下降使用的是如下公式：对比LSTM中$c$的的更新公式$c^{t}=z^{f}\odot c^{t-1}+z^{i}\odot z$，我们很容易发现两者的结构有相通之处，由此产生灵感，我们是否可以把这里的$z^{f}$和$z^{i}$也变成可以学习的呢。也就是输入$\theta ^{t-1}$和$-\bigtriangledown _{\theta }l$，不人为设定$z^{f}$和$z^{i}$，直接输出$\theta ^{t}$。
于是就有了如下方法。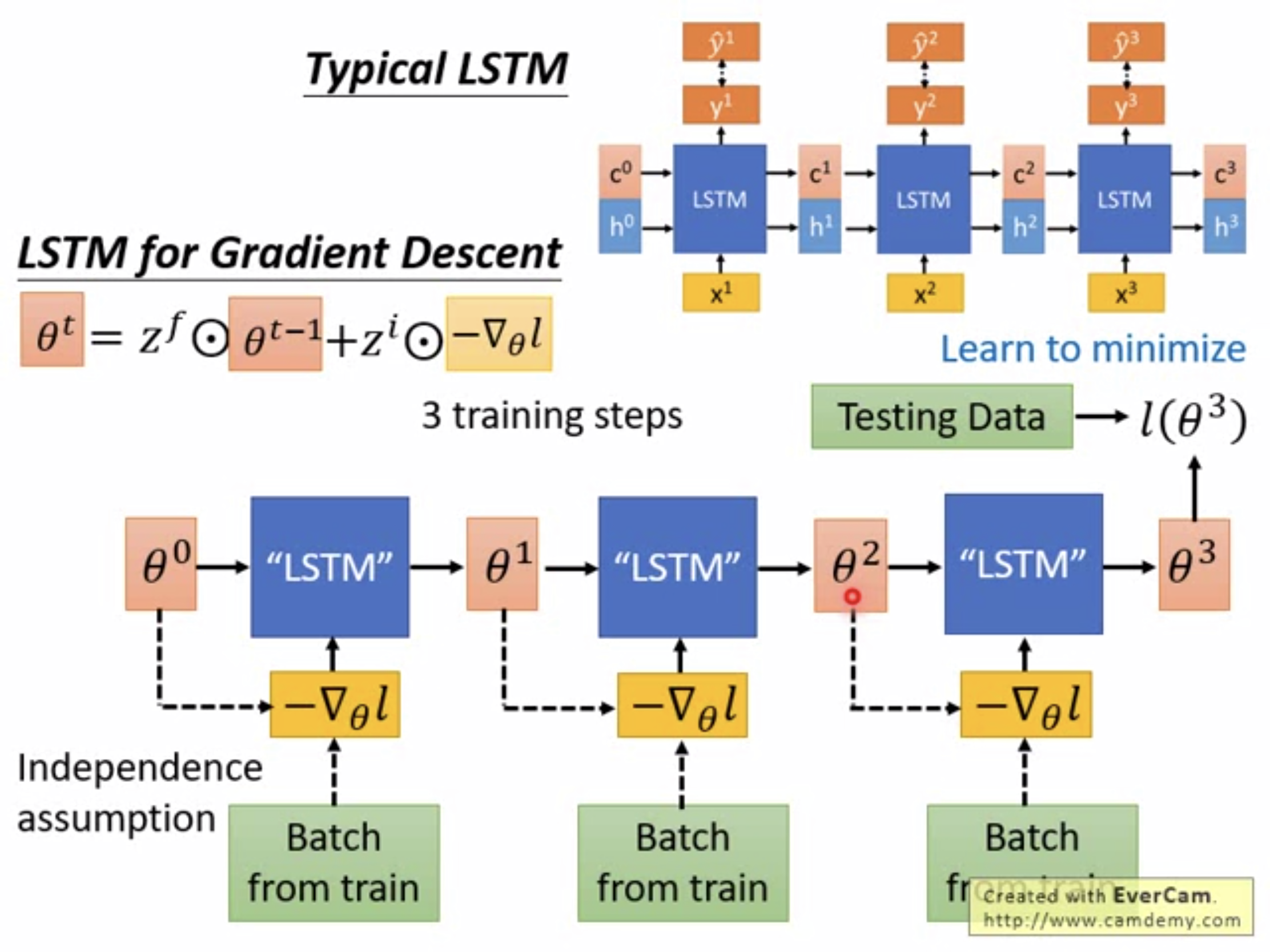
但是，由于$-\bigtriangledown _{\theta }l$的计算依赖于$\theta ^{t-1}$（上图虚线表示），这在反向传播时会比较复杂，因此为了简化，在反向传播时不考虑$-\bigtriangledown _{\theta }l$对$\theta ^{t-1}$的依赖。 
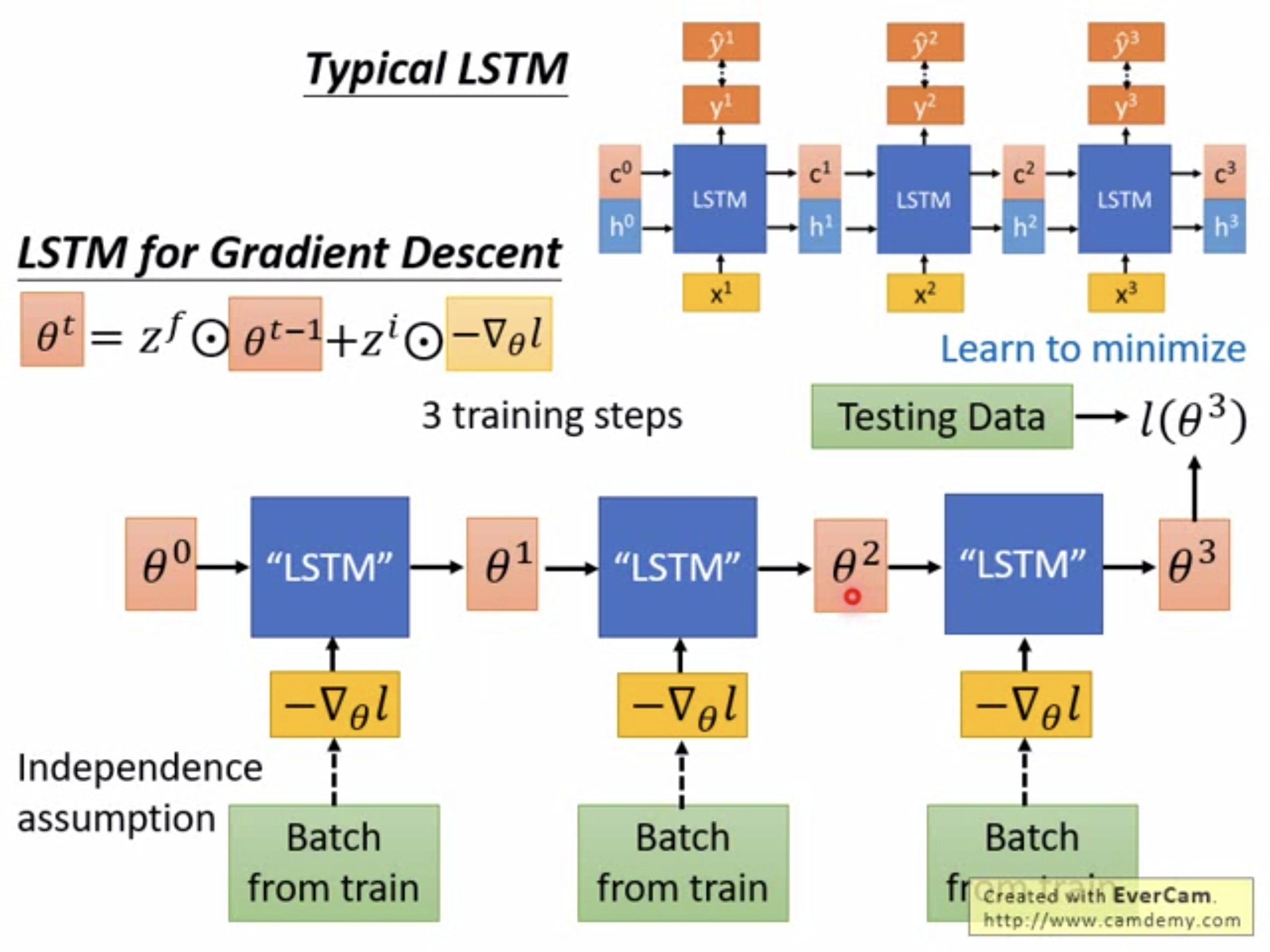注意，如果对所有的参数都设计这样一种学习如何更新的方式，那么计算量是非常大的，因此我们往往对所有参数采用同一套学习出来的更新方式。这是合理的，因为往往我们也会对所有参数设置同样的学习率。
作者对此进行实验来看一看$z^{f}$和$z^{i}$的学习结果究竟如何。如下所示，可见$z^{f}$最后还是收敛到了1，而$z^{i}$也集中在1附近，但也的确学到了一些不一样的信息。
该实验可以表明，我们一般使用的梯度下降公式是比较合理的。不过这里元学习的方法并不是没有作用，后面会提到它的效果。方法2
为了利用更多以往的“记忆”，也可以设计一种两层的LSTM，如下图所示。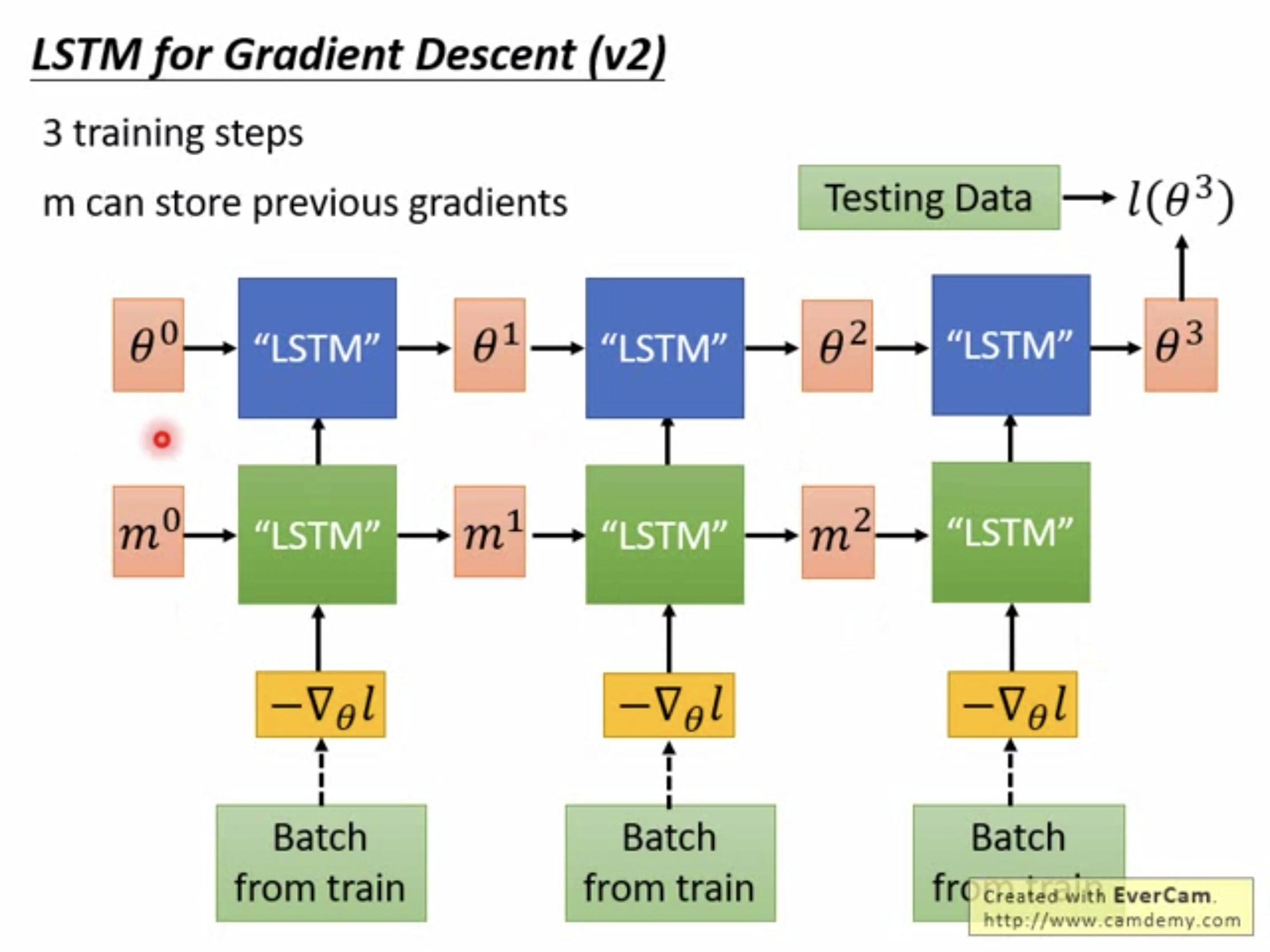
实际上，LSTM这种循环序列模型本身就有利用过往记忆的功能，我将在下一节做更多的介绍。效果
其实这些方法还是比较难实现的，这里来看一下利用LSTM来更新参数最后的效果。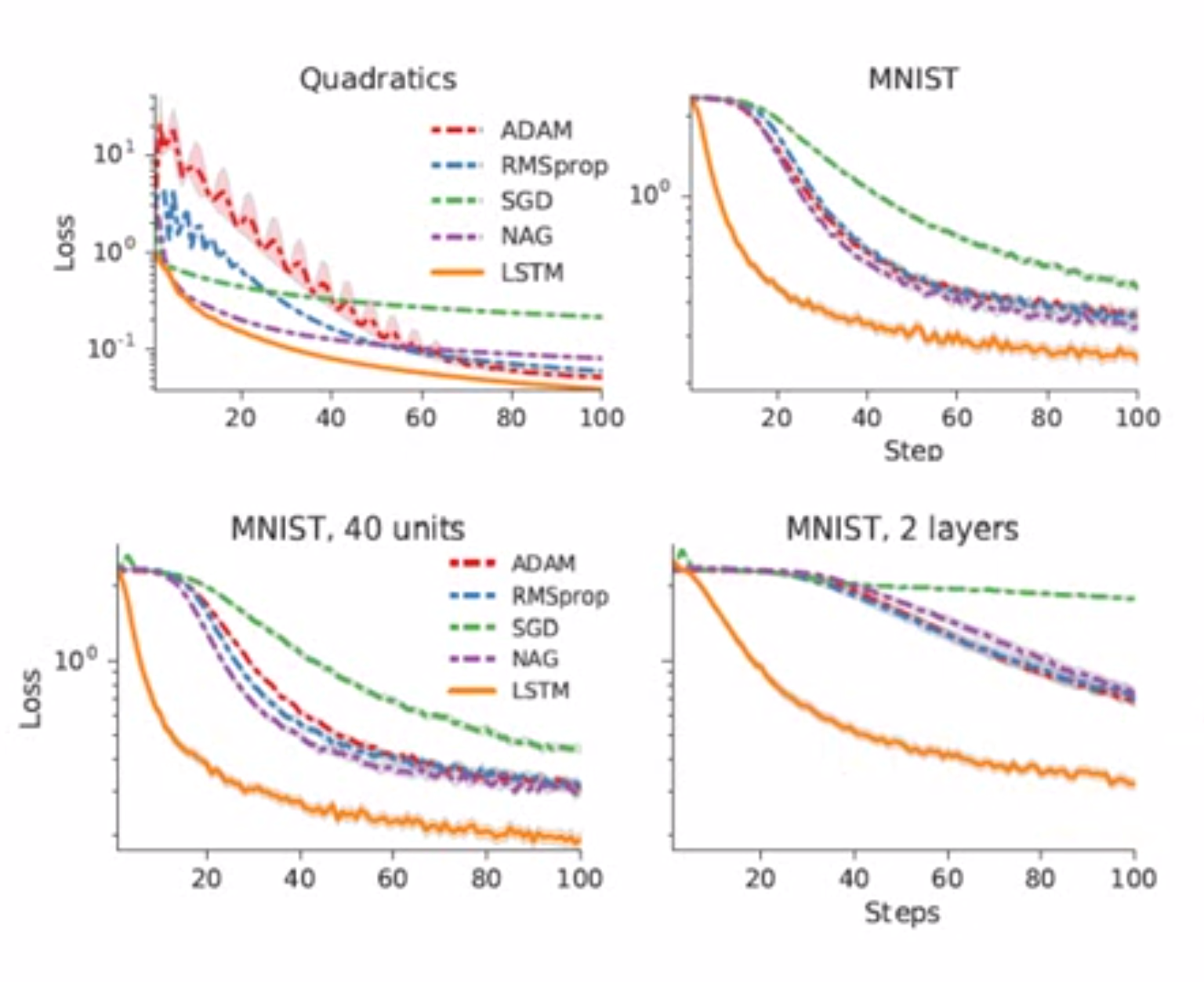
可以看到，这种方法在各种优化算法面前还是有明显的优势的。这里有一个问题是作者进行的实验都是在MNIST数据集上进行的，比如说这里Meta Learning的Training Tasks是识别0，1，2，3…7，Testing Tasks是识别8，9。其实这些任务是同一类任务。作者也注意到了这一点，因此他在训练时用的是20units，测试时使用了40units；训练时只用了1个layer，测试时用了2个layer。以此来证明利用LSTM来更新参数这种方法在不同的模型中的能力。预测梯度
既然Meta Learning的目的是实现快速学习，而快速学习的关键就是神经网络的梯度下降要准且快，那么是否可以让神经网络利用以往的任务学习如何预测梯度，这样面对新的任务，只要梯度预测得准，那么学习得就会更快。
在Learning to Learn by Gradient Descent by Gradient Descent一文中（好好品味这个题目），作者提出了这样一种方法，即训练一个通用的神经网络来预测梯度，用一次二次方程的回归问题来训练，这种方法得到的神经网络优化算法比Adam、RMSProp还要好。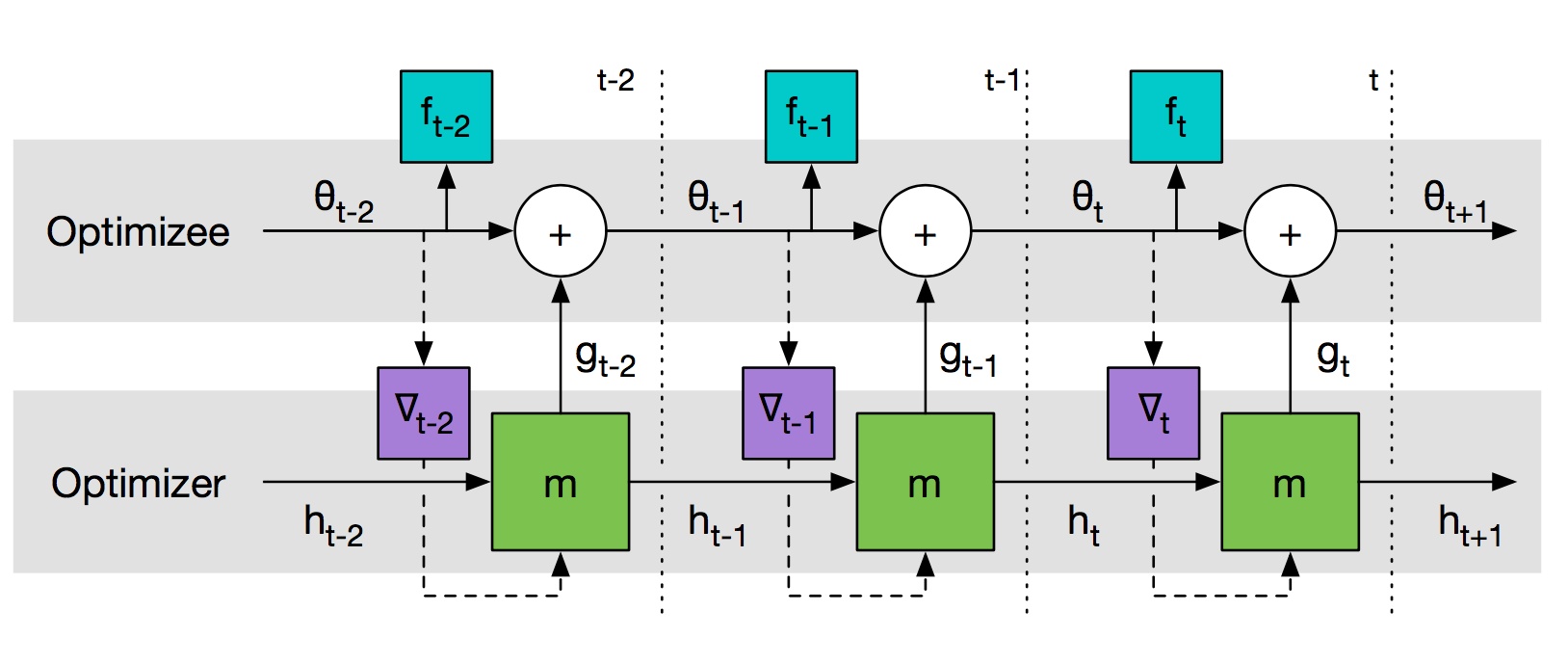
学习记忆的学习
元学习其实也可以利用以往的经验来学习，于是这又诞生了一系列模型。
记忆增强神经网络
一般的神经网络不具有记忆功能，输出的结果只基于当前的输入。而LSTM网络的出现则让网络有了记忆，它能够根据之前的输入给出当前的输出。但是，LSTM的记忆程度并不是那么理想，对于比较长的输入序列，LSTM的最终输出只与最后的几步输入有关，也就是long dependency问题，当然这个问题可以由注意力机制解决，然而还是不能从根本上解决长期记忆的问题，原因是由于LSTM是假设在时间序列上的输入输出：由t-1时刻得到t时刻的输出，然后再循环输入t时刻的结果得到t+1时刻的输出，这样势必会使处于前面序列的输入被淹没，导致这部分记忆被“丢掉”。
基于以上问题，研究者们提出了神经图灵机等记忆增强神经网络模型。我们知道，人除了用脑子记，还会使用做笔记等方式做辅助，当我们忘记时，我们可以去看笔记来获得相关的记忆。记忆增强神经网络的思想就是如此，它让所有的笔记的“读”“写”操作都可微分化，因此可以用神经网络误差后向传播的方式去训练模型。
在记忆增强神经网络中，我们引入外部存储器来存储样本表示和类标签信息。以Meta-Learning with Memory-augmented Neural Networks这篇文章为例，我们看一下它的网络结构。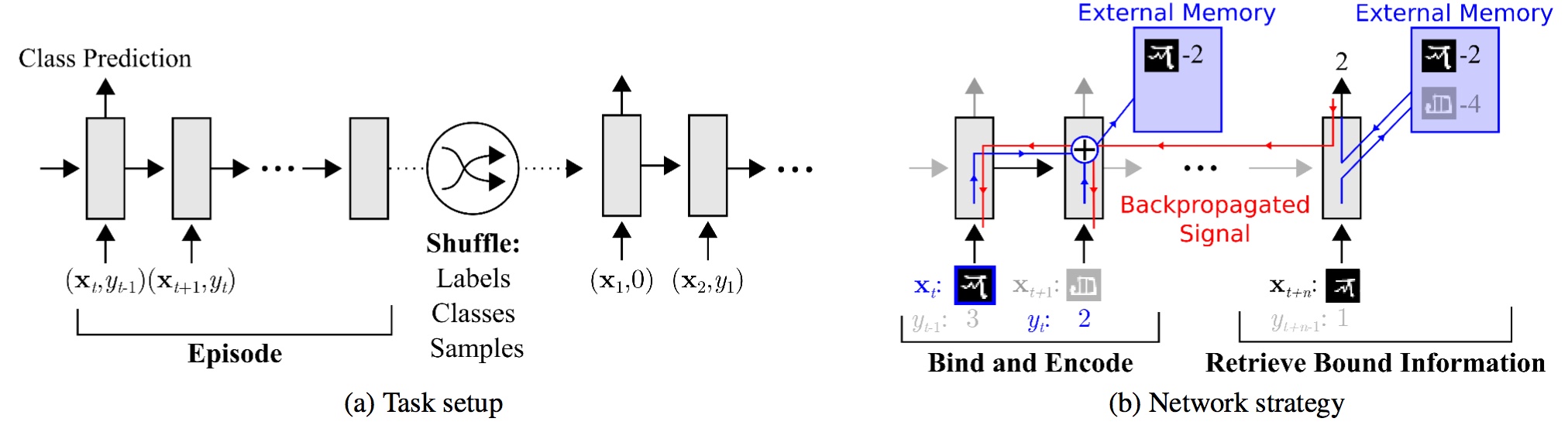
我们可以看到，网络的输入把上一次的y label也作为输入，并且添加了external memory存储上一次的x输入，这使得下一次输入后进行反向传播时，可以让y label和x建立联系，使得之后的x能够通过外部记忆获取相关图像进行比对来实现更好的预测。
WaveNet
WaveNet的网络每次都利用了之前的数据，因此可以考虑WaveNet的方式来实现Meta Learning。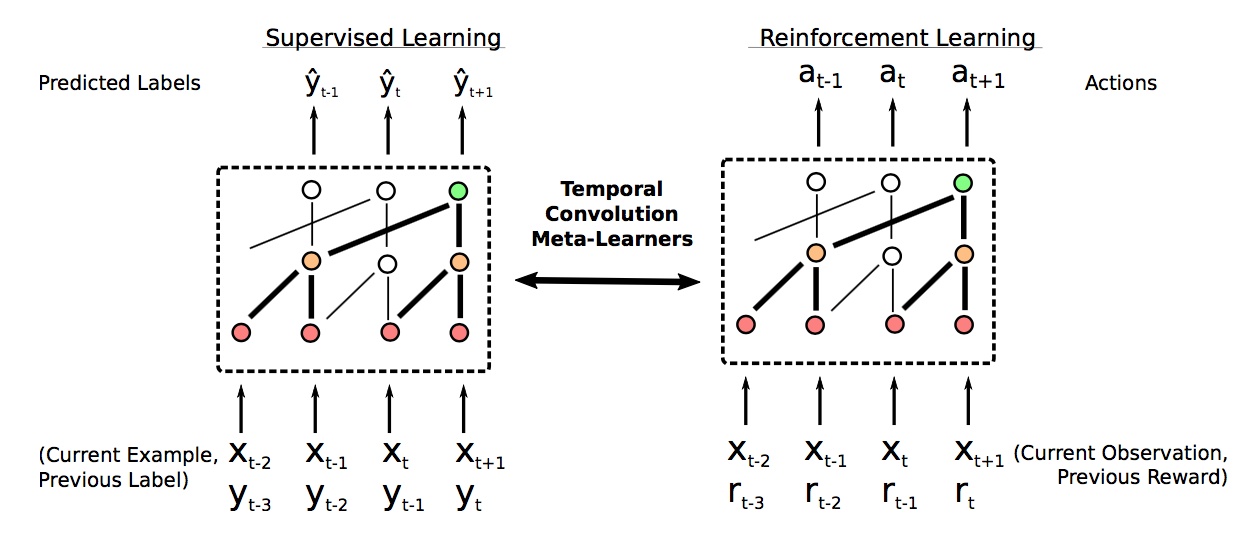
SNAIL
SNAIL意为蜗牛（为什么这么多动物名…），其实直接把论文标题缩写之后和SNAIL是不一样的，之所以命名成SNAIL可能是因为网络结构有点像蜗牛吧。
时序卷积
时序卷积是通过在时间维度上膨胀的一维卷积生成时序数据的结构，如下图所示。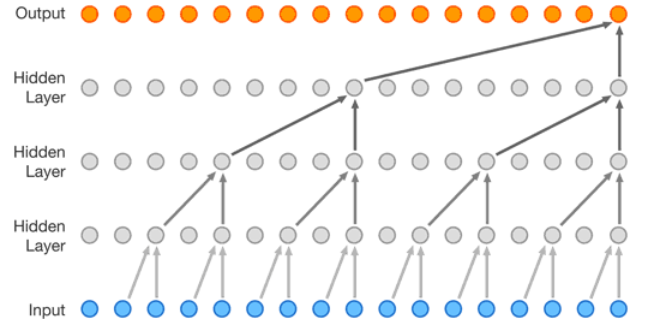
这种时序卷积是因果的，所以在下一个时间节点生成的值只会被之前时间节点的信息影响，而不受未来信息的影响。相比较于传统的RNN，它提供了一种更直接，更高带宽的方式来获取过去的信息。但是，为了处理更长的序列，膨胀率通常是指数级增长的，所以需要的卷积层数和序列长度呈对数关系。因此，只能对很久之前的信息进行粗略的访问，有限的容量和位置依赖性对于元学习方法是不利的，不能充分利用大量的先前的经验。注意力模块
注意力模块可以让模型在可能的无限大的上下文中精确的定位信息，把上下文信息当做无序的键值对，通过内容对其进行查找。网络
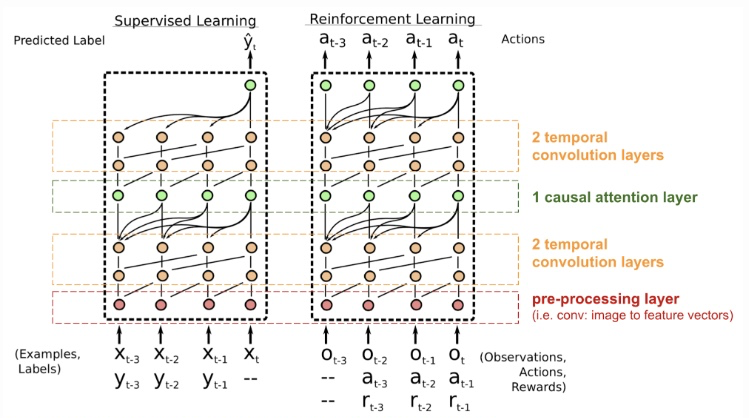SNAIL由两个时序卷积和attention交错组成。时序卷积可以在有限的上下文中提供高带宽的访问方式，attention可以在很大的上下文中精确地访问信息，所以将二者结合起来就得到了SNAIL。在时序卷积产生的上下文中应用causal attention，可以使网络学习应该挑选聚集哪些信息，以及如何更好地表示这些信息。注意：英语小贴士，因果：causal；休闲：casual。
学习方法的学习
元学习还用于对数据处理中的一些方法进行学习，比如这里要介绍的对特征提取方法的学习。
Siamese Network孪生网络
Siamese Network中文译为孪生网络。常用于人脸验证（不同于人脸识别），近几年在目标跟踪领域也大放光彩。
在Siamese Network中，我们首先使用两个共享模型参数值的相同网络来提取两个样本的特征（也有个别伪Siamese Network，它们不共享网络权重）。然后，我们将提取出的特征输入鉴别器，判断两个样本是否属于同一类对象。例如，我们可以计算其特征向量的余弦相似度（p）。如果它们相似，那么p应该接近1；否则，它们应该接近0。根据样本的标签和p，我们对网络进行相应的训练。简而言之，我们希望找到使样例属于同一类或将它们区分开来的特性。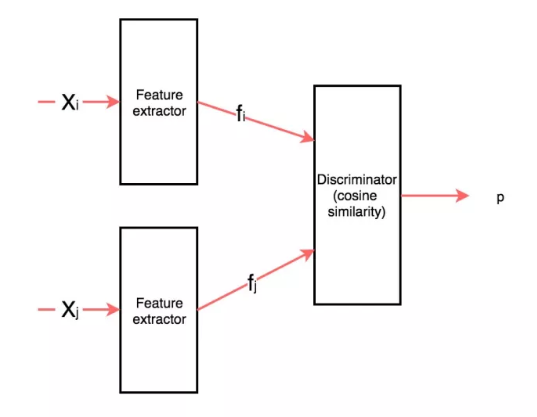
这里利用神经网络的好处是它能够学习到哪些特征是该提取的，比如在一些传统的方法中，它们会对整个图像进行特征转化，其中也将包括背景，这样就可能会导致当两个相似背景但不同对象的图片作为输入时，输出会判定为相同。而神经网络它可以在训练过程中学习到哪些部分是值得关注的，可以学会ignore背景。
李宏毅老师在讲这一块的时候还提到了一种思路，就是学习一种算法（生成网络），这种算法能够使用one-shot learning输入的少量样本生成许多样本用于和prediction的那个输入进行比对验证，其框架与Siamese Network基本相似。
Matching Network匹配网络
Matching Network与Siamese Network十分相似。我们知道，人的注意力是可以利用以往的经验来实现提升的。那么，能不能利用以往的任务来训练一个attention模型，使得模型面对新的任务时，能够直接关注最重要的部分。
于是就有了Matching Network。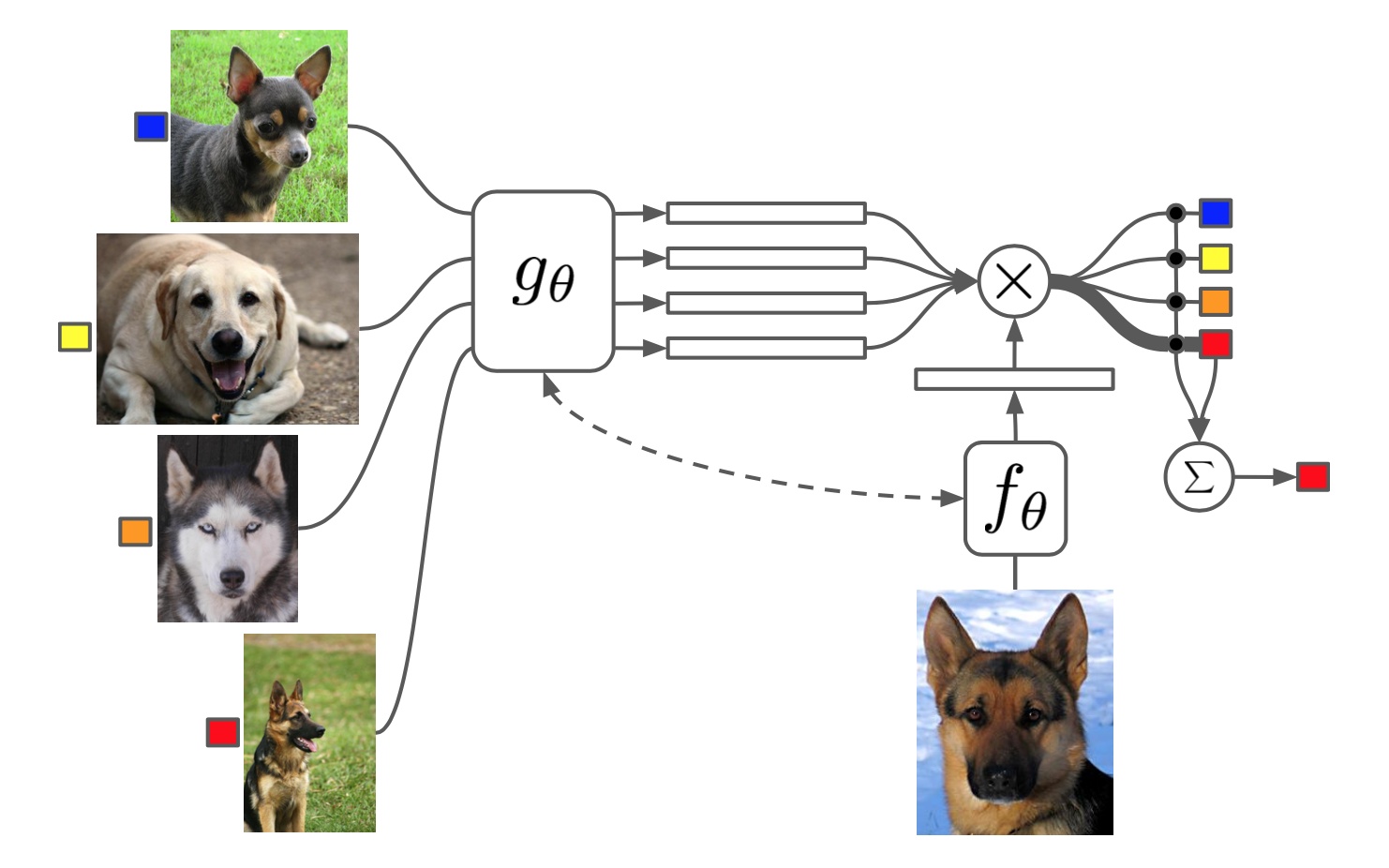
这里的g和f是特征提取器，和Siamese Network一样使用深度网络来提取特征，用于我们的输入和测试样本。通常情况下，g和f是相同的，共享相同的深度网络。然后，我们比较它们的相似度。同样，我们从预测中计算一个损失函数来训练我们的特征提取器。
这里构造了一个attention机制，也就是最后的label判断是通过attention的叠加得到的：
其实这里的网络结构远比上面画出来的复杂（用到了LSTM）。我们可以来看一下它的表现，在Omniglot数据集（找一批人照着象形文字画出来的）上，它取得了比Siamese Network更好一点的成绩。不过具体能力如何，还得看论文跑实验。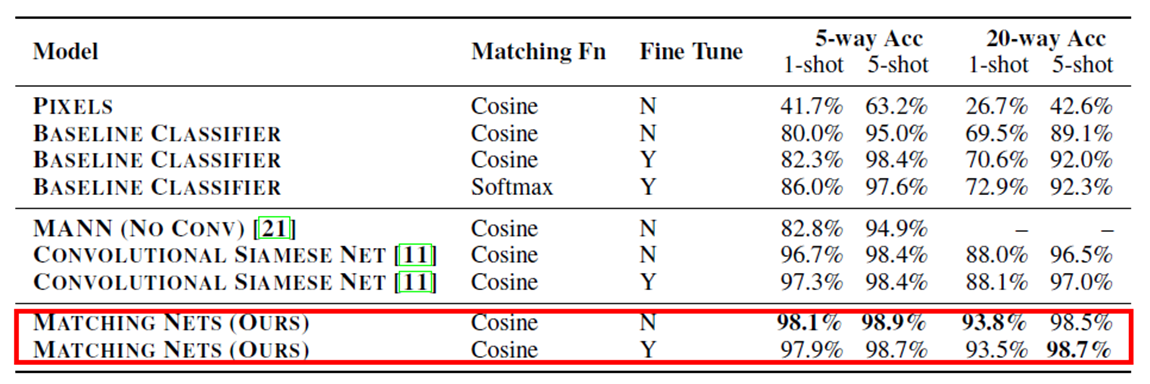
Prototypical Network原型网络
该方法思想十分简单，效果也非常好。它学习的是一个度量空间，通过计算和每个类别的原型表达的距离来进行分类。
具体的思路是：每个类别都存在一个聚在某单个原型表达周围的embedding，该类的原型是Support Set在embedding空间中的均值。然后，分类问题变成在embedding空间中的最近邻。如图所示，c1、c2、c3分别是三个类别的均值中心（称Prototype），将测试样本x进行embedding后，与这3个中心进行距离计算，从而获得x的类别。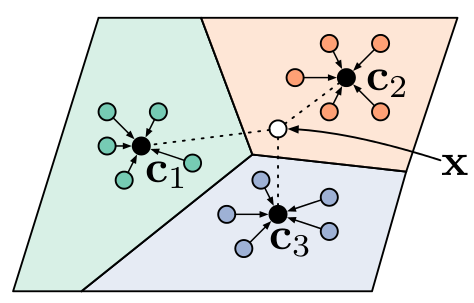
学习损失的学习
前面提到，Meta Learning处理的主要是one-shot learning，而one-shot learning需要让学习的速度更快。学习效率除了用更好的梯度来提高，也可以考虑寻找更好的损失函数。根据这种思路，或许可以构造一个模型利用以往的任务来学习如何预测loss。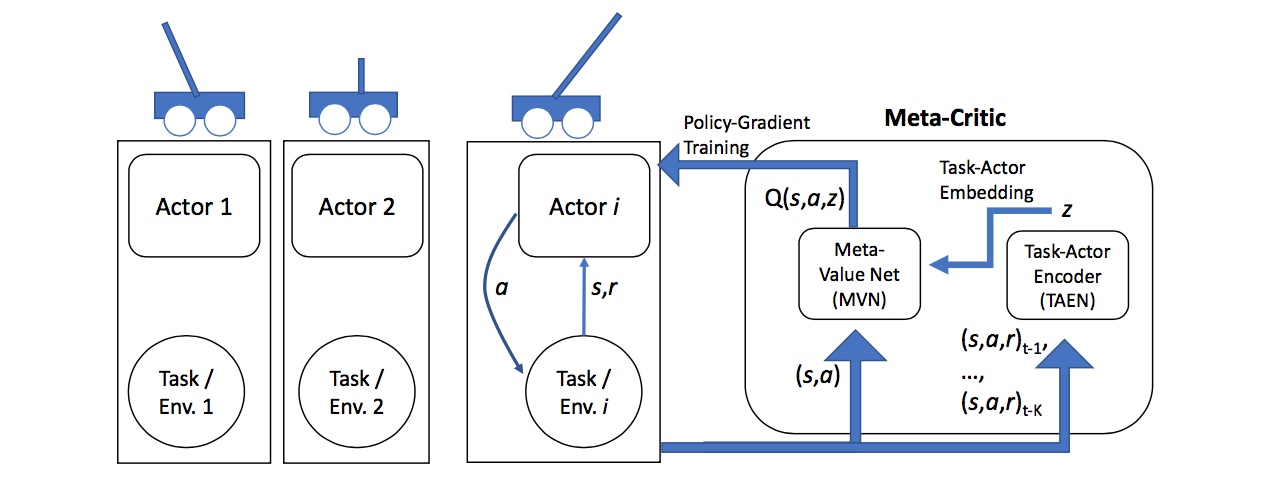
如上图所示，作者构造了一个Meta-Critic Network，其作用是用来学习如何预测Actor Network的loss。这也是一种思路吧。
学习结构的学习
还有一种思路就是结合深度学习动态地生成一个新的模型。
这种方法能使得模型更加准确，但不一定能够更有效地使用较少的样本来学习，不适合用于one-shot learning。
小结
套娃预警！
在古印度神话中，有人问世界在哪？答案是在乌龟的背上。那么乌龟在哪？乌龟在另一个大乌龟的背上。那么大乌龟在哪…
那么，我们之前让机器learn，现在想办法让机器learn to learn，那之后是不是还要learn to learn to learn再learn to learn to learn to learn呢？哈哈套娃警告。
难以想象未来的机器会是怎么样的，如此智能真的有点细思极恐呢。话说回来，Meta Learning方兴未艾，各种神奇的idea层出不穷，但是真正的杀手级算法尚未出现，让我们拭目以待！