之前在deep-learning笔记：学习率衰减与批归一化一文中，我已经对仿射变换作了简单的介绍。但这里我想提出来单独对其做一个小归纳。

应用

仿射变换在计算机科学中有丰富的运用。例如，在计算机图形学中，它可以用于在较小或较大的屏幕上显示图形内容时简单地重新缩放图形内容。此外，它也可以应用于扭曲一个图像到另一个图像平面。
另一个重要的应用是训练深层神经网络时用于扩充数据集。训练深度模型需要大量的数据。在几乎所有的情况下，模型都受益于更高的泛化性能，因为有更多的训练图像。人工生成更多数据的一种方法就是对输入数据随机应用仿射变换（数据增强）。
此外，在模型要求固定尺寸的输入时，仿射变换也是一种主要的解决方案。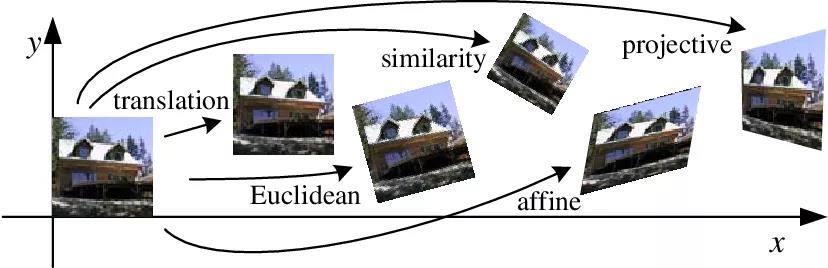
图形变换

仿射变换

二维仿射变换可以用下面这个公式来表示：

$x'=Ax$

其中$A$是在齐次坐标系中的3x3矩阵，$x$是在齐次坐标系中$(x，y，1)$形式的向量。这个公式表示$A$将一个任意向量$x$映射到另一个向量$x’$。
一般来说，仿射变换有6个自由度。根据参数的值，它将在矩阵乘法后扭曲任何图像。变换后的图像保留了原始图像中的平行直线（考虑剪切）。本质上，满足这两个条件的任何变换都是仿射的。它保持了二维图形的“平直性”、“平行性”和“共线比例不变性”，非共线的三对对应点可以确定一个唯一的仿射变换。
下面一些特殊形式的$A$，如下图所示，从上到下分别是：缩放、平移和旋转。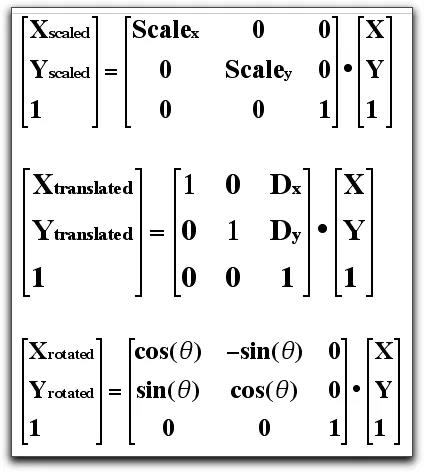

上述仿射变换的一个非常有用的性质是它们是线性函数。它们保留了乘法和加法运算，并遵循叠加原理。

换言之，我们可以组合2个或更多的变换：向量加法表示平移，矩阵乘法表示线性映射，只要我们用齐次坐标表示它们。即利用这个性质，我们可以将二维仿射变换视为线性变换R和平移变换T的叠加，具体可以看一下之前的文章。
举个例子，我们可以将旋转和平移如下表示：

1
2
3

A = array([[cos(angle), -sin(angle), tx],
           [sin(angle), cos(angle),  ty],
           [0,          0,           1]])

如果理解了的话，你会发现各种各样的变化其实还挺繁琐的。不过请放心，大多数开发人员和研究人员通常省去了编写所有这些变换的麻烦，而只需依赖优化的库来执行任务。在OpenCV中进行仿射变换非常简单，如果今后遇到的比较多再做整理。

之前在artificial-intelligence笔记：吴恩达——阅读论文的建议一文中提到以后会分享几个觉得有价值的公众号的，这里就再分享一个吧。本文中的图片均来自该公众号的推文。
磬创AI