linear algebra笔记：循环矩阵

循环矩阵是我在看相关滤波时遇到的一个terminology，通过一定的了解之后发现其具有许多有用的性质。在目标跟踪领域，循环矩阵的引入对速度的提升是非常大的。关于相关滤波，由于现在了解还不够全面和深入，暂时不提及。本文主要就循环矩阵的概念和性质做一个总结。

References：

电子文献：
https://www.cnblogs.com/cj-xxz/p/10323711.html
https://blog.csdn.net/shenxiaolu1984/article/details/50884830

参考文献：
[1]High-Speed Tracking with Kernelized Correlation Filters

---

循环矩阵（Circulant Matrices）

任意循环矩阵可以被傅里叶变换矩阵对角化。（All circulant matrices are made diagonal by the Discrete Fourier Transform (DFT), regardless of the generating vector x.）我们在文献中往往会看到这样一个变换：

$$X=C(x)=F\cdot diag(\widehat{x})\cdot F^{H}$$

下面的$X$它就是一个循环矩阵，它是由它的第一行$x=(x_{1},x_{2},…,x_{n})$的向量组每次经过一个循环移位，得到的一个循环矩阵。其中$\widehat{x}$（读作x hat）为原向量$x$的傅里叶变换；$F$是傅里叶变换矩阵，$F^{H}$表示共轭转置。
换句话说，循环矩阵$X$相似于对角阵，其特征值是$\widehat{x}$的元素。以长度为3的$x$为例，其生成的循环矩阵为：

$$X=C(x)=\begin{bmatrix} x_{1} & x_{2} & x_{3}\\ x_{3} & x_{1} & x_{2}\\ x_{2} & x_{3} & x_{1} \end{bmatrix}$$

这样的一个矩阵它有一个特别好的性质，就是能够通过它的第一行的生成向量来做来进行对角化。通过这个式子，我们能够把$X$循环矩阵进行对角化，如此把它转换到傅里叶域之后，用离散傅里叶变化来做运算时，对速度的提升是非常大的，这将在后文进一步说明。

关于这里的对角化、傅里叶变换矩阵可以看后文，在此先跳过。

这里有必要列出循环矩阵的两个重要公式，这两个性质是比较常用和有用的：

1. 卷积

   循环矩阵乘向量等价于生成向量的逆序和该向量卷积，可进一步转化为傅里叶变换相乘。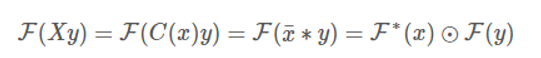 这里$\overline{x}$表示$x$的逆序排列，$*$表示共轭。

   注意：卷积本身也包含逆序操作。此外，这里最后一个等号利用了信号与系统中的“时域卷积，频域相乘”，即时域卷积定理，它表明两信号在时域的卷积积分对应于在频域中该两信号的傅里叶变换的乘积。

2. 相乘

   循环矩阵的乘积仍是循环矩阵，所以我们只要维护循环矩阵的第一行，就可以以较低的复杂度维护循环矩阵的乘积。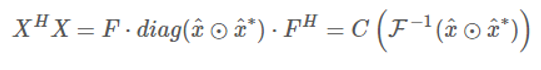 公式中最终所得的乘积也是循环矩阵，其生成向量是原生成向量对位相乘的傅里叶逆变换。

用了上述循环矩阵的性质之后，我们就可以使得原来两个矩阵相乘的时间复杂度$O(K^{3})$能够降到$O(Klog(K))$（反向傅里叶的复杂度（$O(Klog(K))$）加上向量点乘的复杂度（$K$）），速度的提升是非常明显的。

注：这里K表示的是矩阵的尺寸。

在非线形的情况下，当引入了核之后，也可以得到同样的一个情况。此时需要这个核满足一定的条件，它是可以具备循环矩阵的一些性质的，例如常用的高斯核、线性核都满足这个条件，因此可以直接拿来用。

---

傅里叶变换矩阵（DFT matrix）

关于离散傅里叶矩阵$F$这里涉及较多的数学，想看详细推导可以参考文首给出的第二个参考链接。这里把比较关键的结论部分截了过来。

$F$在这里是一个奇异矩阵（方阵且行列式等于零），它可以对任意输入向量进行傅里叶变换，这是因为傅里叶变换具有线性性。

---

矩阵快速幂

在本文前的第一个参考链接中，作者是用矩阵快速幂引入的，那么这里我也简单谈一下快速幂。
顾名思义，快速幂就是快速算某个数的多少次幂。
我们知道，对于任何一个整数，都能用二进制来表示。那么对于$a^{n}$，$n$也一定可以用二进制来表示。
那么问题来了，如何计算某个数较大的次幂呢？
比如计算$a^{156}$，我们可以利用除二取余、倒序排列、高位补零的方法得到$(156)_{10}=(10011100)_{2}$。
如此可以推导：

$$Ans=a^{(156)_{10}}=a^{(10011100)_{2}}$$ $$=a^{2^{7}*1+2^{6}*0+2^{5}*0+2^{4}*1+2^{3}*1+2^{2}*1+2^{1}*0+2^{0}*0}$$ $$=(a^{2^{7}})*(a^{2^{4}})*(a^{2^{3}})*(a^{2^{2}})$$

这样一来，原本要进行$156-1=155$次乘法运算，现在运算量级相当于该幂的二进制数表示中1的个数。其时间复杂度为$O(log_{2}n)$，与朴素的$O(n)$相比，效率有了极大地提高。
以上就是一般的快速幂的基本套路。相对于一般的快速幂，矩阵快速幂仅仅是把他的底数和乘数换成了矩阵形式。其主要方法就是：通过把数放到矩阵的不同位置，然后把普通递推式构造成类似于“矩阵的等比数列”，最后快速幂求解递推式。
矩阵快速幂主要用于求一个很复杂的递推式中的某一项问题。
递推矩阵（关系矩阵）的构造，也是矩阵快速幂的难点，一般是由原始的递推公式推导或者配凑得出，网上有许多ACM的赛题解答，可以看几道理解一下思路。