machine learning笔记：SVD与字典学习

SVD，译为奇异值分解，是一种常用的数据降维方式。一般我们可以对实兑成矩阵作特征值分解，而SVD就类似于对一般情况下MxN的实数矩阵作“特征值分解”，称结果中对角线上的值为奇异值。
而字典学习（Dictionary Learning），又叫KSVD，是一种常用的稀疏表示方法，其本质就是经过K轮迭代，而每次迭代都使用SVD来降维。

---

分享

SVD
字典学习
关于SVD和字典学习，这位博主的这两篇文章写得很棒，思路清晰准确，尤其是排版让人赏心悦目。自己功力不足，又怕放在收藏夹里吃灰，附链接在此方便日后学习。

---

代码实现

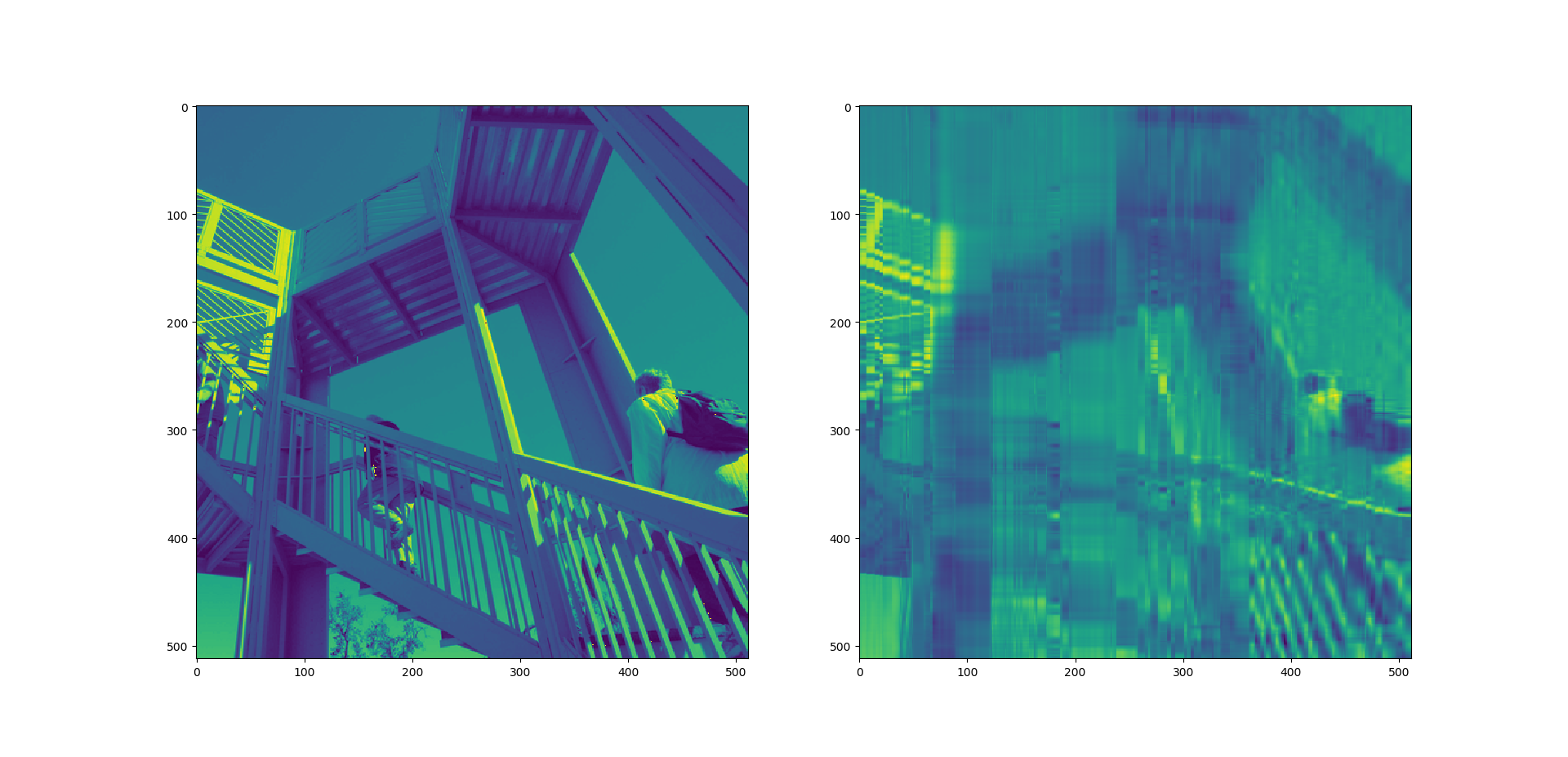
这里以scipy库中提供的样本图片为例（原本有计算机视觉女生Lena，现换成了一张爬楼梯图），对字典学习的实现过程做一个比较简单的展示和比较详细的注释。

#基本准备
import numpy as np #待会直接调用numpy.linalg.svd函数来实现SVD
from sklearn import linear_model
import scipy.misc #这是一个图像处理的库，待会需借用其中的图片样本
import matplotlib.pyplot as plt #画图要用

#稀疏模型Y = DX，Y为样本矩阵，使用KSVD动态更新字典矩阵D和稀疏矩阵X

class KSVD(object): #单继承object()的属性
    def __init__(self, n_components, max_iter = 30, tol = 1e-6,
                 n_nonzero_coefs = None):
        self.dictionary = None
        self.sparsecode = None
        self.max_iter = max_iter #最大迭代次数
        self.tol = tol #稀疏表示结果的容差
        self.n_components = n_components #字典所含原子个数（字典的列数）
        self.n_nonzero_coefs = n_nonzero_coefs #稀疏度

    #初始化字典矩阵
    def _initialize(self, y):
        u, s, v = np.linalg.svd(y)
        self.dictionary = u[:, :self.n_components]

    #使用KSVD更新字典的过程
    def _update_dict(self, y, d, x):
        for i in range(self.n_components):
            #选择X中第i行（从0开始）中非零项
            index = np.nonzero(x[i, :])[0]
            #如果没有非零项，则直接进入下一次for循环
            if len(index) == 0:
                continue
                
            #更新D中第i列
            d[:, i] = 0
            #计算误差矩阵
            r = (y - np.dot(d, x))[:, index]
            #利用SVD的方法，来求解更新字典和稀疏系数矩阵
            u, s, v = np.linalg.svd(r, full_matrices = False)
            #使用左奇异矩阵的第0列更新字典
            d[:, i] = u[:, 0].T
            #使用第0个奇异值和右奇异矩阵的第0行的乘积更新稀疏系数矩阵
            x[i, index] = s[0] * v[0, :]
        return d, x

    #KSVD迭代过程
    def fit(self, y):
        self._initialize(y)
        for i in range(self.max_iter): #在最大迭代范围内
            #稀疏编码
            x = linear_model.orthogonal_mp(self.dictionary, y, n_nonzero_coefs = self.n_nonzero_coefs)
            #计算容差
            e = np.linalg.norm(y - np.dot(self.dictionary, x))
            #满足容差就结束
            if e < self.tol:
                break
            #更新字典
            self._update_dict(y, self.dictionary, x)

        #稀疏编码
        self.sparsecode = linear_model.orthogonal_mp(self.dictionary, y, n_nonzero_coefs = self.n_nonzero_coefs)

        return self.dictionary, self.sparsecode


if __name__ == '__main__': #作为脚本时直接执行，但被import至其它脚本时不会被执行
    #调用scipy中的爬楼梯图
    im_ascent = scipy.misc.ascent().astype(np.float)
    ksvd = KSVD(100) #100列的字典
    dictionary, sparsecode = ksvd.fit(im_ascent)

    plt.figure()
    #创建子图，1行2列中的第1张图片
    plt.subplot(1, 2, 1)
    plt.imshow(im_ascent) #原图
    #创建子图，1行2列中的第2张图片
    plt.subplot(1, 2, 2)
    plt.imshow(dictionary.dot(sparsecode))
    #dictionary.dot(sparsecode)等价于numpy.dot(dictionary, sparsecode)，即矩阵相乘，这里是DX = Y
    plt.show()

以下是字典中“词汇量”（即可表示属性的个数）不同时的三种结果。