matlab笔记：一个非线性方程问题的多种求解方法

发表于 | 更新于: | 分类于 | | 阅读次数:
字数统计: 3.1k字 | 阅读时长 ≈ 12分钟

上周科学计算引论结课了，借着写上机报告的机会，我把书本上所有的求解非线性方程的方法（标量型）都用matlab实现了一下，并对一个实际工程问题进行求解。关于实现过程中遇到的问题以及注意事项，我已写在matlab笔记：久未使用之后踩的一堆坑内。

实际问题

在电机学中，凸极同步发电机的功角特性可表示为：

式中，$P_{em}$表示发电机的电磁功率；$E_{0}$表示发电机电势；$V$表示发电机端电压；$x_{q}$表示横轴同步电抗；$x_{d}$表示纵轴同步电抗；$\theta$表示功率角，$\theta \in \left ( 0,\frac{\pi }{2} \right )$。
如令$\frac{E_{0}V}{x_{d}}=P_{j}$，$V^{2}\left ( \frac{1}{x_{q}}-\frac{1}{x_{d}} \right )=P_{2e}$，则上式可以简化为：

在电力系统稳定计算中，我们往往要由上式求出功率角$\theta$。我们可以使用几何方法求解，也可以利用迭代法求解该非线性方程。
我们将上式变为：

以许实章编《电机学习题集》第367页26-1为例，将$P_{em}=1$，$P_{j}=1.878$，$P_{2e}=0.75$代入，得到方程：

问题求解

在《计算方法》第二章，我们学习了一些非线性方程的数值解法，这里我们分别使用几何法和迭代法求解上述问题并进行比较。设方程求解的预定精度为$0.001^{\circ}$即$1.7\times 10^{-3}rad$，由闭区间上连续函数的性质和初步估计，可确定方程的解位于区间$[0,\frac{\pi }{6}]$。

几何方法

由几何法的求解方法，我们定义函数：

求解$\theta$即求解$f(\theta )$在$[0,\frac{\pi }{6}]$上的零点。
在matlab中，将该函数实现如下：

1
2
3
4
5
6
function [y] = func(x)
%几何法函数方程
%统一使用弧度制
format long %为提高精度，保留更多位数
y = asin(1 / (1.878 + 0.75 * cos(x))) - x;
end

由于matlab计算过程中默认保留$4$位小数，为了提高精度，我使用了format long保留更多有效数字。值得注意的是，计算时统一使用弧度制，待求出解之后再使用rad2deg函数转化为角度。

二分法

根据二分法的格式，编写二分法函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function [errors, ans, time] = bisection(low, high, max, stopError) 
%二分法
%func是待求零点的函数
%low，high分别是解区间的上下限
%max是最多循环步数，防止死循环
%stopError是预定精度，作为终止条件
%errors记录每次循环的误差
%ans记录最终求解结果，表示为角度
%time是总的循环次数
format long %为提高精度，保留更多位数
fl = func(low);
fh = func(high);
error = high - low;
for i = 1 : max
    mid = (low + high ) / 2;
    fm = func(mid);    
    if fm * fl > 0
        low = mid;
    else high = mid;
    end
error = high - low;
errors(i) = error;
    if error < stopError, break, end
end
time = i;
ans = rad2deg(mid); %转换成角度
end

输入命令[errorsB, ans, time] = bisection(0, pi / 6, 50, 1.7e-5)，求得结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
errorsB =

  列 1 至 5

   0.261799387799149   0.130899693899575   0.065449846949787   0.032724923474894   0.016362461737447

  列 6 至 10

   0.008181230868723   0.004090615434362   0.002045307717181   0.001022653858590   0.000511326929295

  列 11 至 15

   0.000255663464648   0.000127831732324   0.000063915866162   0.000031957933081   0.000015978966540


ans =

  22.909240722656250


time =

    15

使用二分法共迭代$15$次，求得结果为$22.909240722656250^{\circ}$。此外，迭代误差为$0.000015978966540$，符合预设精度要求。然而，此种方法计算次数较多，因此我又尝试了下面的方法。

弦截法

根据弦截法的计算方法，编写弦截法函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function [errors, ans, time] = linecut(a, b, max, stopError)
%弦截法
%func是待求零点的函数
%a，b是在解的领域取的两点，这里取解区间的两个端点
%max是最多循环步数，防止死循环
%stopError是预定精度，作为终止条件
%errors记录每次循环的误差
%ans记录最终求解结果，表示为角度
%time是总的循环次数
format long %为提高精度，保留更多位数
fa = func(a);
fb = func(b);
error = abs(a - b); 
for i = 1 : max
    x = b - (b - a) * fb / (fb - fa);
    a = b;
    b = x;
    fa = func(a);
    fb = func(b);
    error = abs(a - b);
    errors(i) = error;
    if error < stopError, break, end
end
time = i;
ans = rad2deg(b); %转换成角度
end

输入命令[errorsL, ans, time] = linecut(0, pi / 6, 50, 1.7e-5)，求得结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
errorsL =

   0.120609794441825   0.003164447033051   0.000026217912123   0.000000005427336


ans =

  22.909760215805360


time =

     4

与上面的二分法相比，弦截法只需计算$4$次，效率大大提高。计算所得结果为$22.909760215805360^{\circ}$，迭代误差为$0.000000005427336$，符合预设精度要求，而且比二分法的最终迭代误差更小，显然可以发现弦截法的收敛速度要快于二分法。下面我再用弦截法的改造方法Steffensen方法进行试验。

Steffensen方法

根据Steffensen方法的计算方法，编写函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
function [errors, ans, time] = steffensen(x, max, stopError)
%Steffensen方法
%func是待求零点的函数
%x是初始点
%max是最多循环步数，防止死循环
%stopError是预定精度，作为终止条件
%errors记录每次循环的误差
%ans记录最终求解结果，表示为角度
%time是总的循环次数
format long %为提高精度，保留更多位数
f = func(x);
for i = 1 : max
    o = x - f ^ 2 / (f - func(x - f));
    error = abs(x - o);
    x = o;
    f = func(o);
    errors(i) = error;
    if error < stopError, break, end
end
time = i;
ans = rad2deg(o); %转换成角度
end

选取初始点为$0$，输入命令[errorsS1, ans, time] = steffensen(0, 50, 1.7e-5)，求得结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
errorsS1 =

   0.381516143583955   0.018291709371805   0.000042893415627   0.000000000236814


ans =

  22.909760215804820


time =

     4

发现计算次数没有比弦截法少，因此修改初值为$\frac{\pi }{6}$，再次计算，得结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
errorsS2 =

   0.125855705283236   0.002107105082521   0.000000571210576


ans =

  22.909760215802425


time =

     3

一般而言，Steffensen方法的收敛速度要快于弦截法，但这与初始点的选取有关。对于这个问题，当设初始点为$0$时，Steffensen方法的迭代次数与弦截法持平；当设初始点为$\frac{\pi }{6}$时，迭代次数才小于弦截法。因此，想让Steffensen方法更快地收敛，需选取合适的初始点。在我看来，Steffensen方法的一大优势就是它是一种单步迭代方法，相比二步迭代方法的弦截法，Steffensen方法只需要一个初值就可以开始迭代。

Picard迭代法

上述的方法都是基于几何图形的求解方法，而下面的Picard迭代法则是基于不动点原理给出的。
首先，我们编写迭代函数：

1
2
3
4
5
6
function [y] = interation(x)
%迭代函数
%统一使用弧度制
format long %为提高精度，保留更多位数
y = asin(1 / (1.878 + 0.75 * cos(x)));
end

我们使用如下命令查看函数图像：

1
2
3
>> x = 0 : pi / 36 : pi / 6;
>> y = asin(1 * (1.878 + 0.75 * cos(x)) .^ (-1));
>> plot(x, y)

得到：

易验证，该函数在$[0,\frac{\pi }{6}]$上满足Picard迭代条件。

Picard迭代法

根据Picard迭代法原理，定义Picard迭代函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function [errors, ans, time] = picard(x, max, stopError)
%Picard迭代法
%interation是迭代函数
%x是初始点
%max是最多循环步数，防止死循环
%stopError是预定精度，作为终止条件
%errors记录每次循环的误差
%ans记录最终求解结果，表示为角度
%time是总的循环次数
format long %为提高精度，保留更多位数
for i = 1 : max
    o = interation(x);
    error = abs(x - o);
    x = o;
    errors(i) = error;
    if error < stopError, break, end
end
time = i;
ans = rad2deg(o); %转换成角度
end

输入命令[errorsP, ans, time] = picard(0, 50, 1.7e-5)求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
errorsP =

   0.390355832559508   0.009044503640668   0.000428788831489   0.000020583068808   0.000000988625736


ans =

  22.909757357777192


time =

     5

Picard迭代结果为$22.909757357777192^{\circ}$，且精度符合要求。下面使用Picard迭代法的改进Aitken加速迭代法进行试验。

Aitken加速迭代法

编写Aitken加速迭代法函数代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
function [errors, ans, time] = aitken(x, max, stopError)
%Aitken迭代法
%interation是迭代函数
%x是初始点
%max是最多循环步数，防止死循环
%stopError是预定精度，作为终止条件
%errors记录每次循环的误差
%ans记录最终求解结果，表示为角度
%time是总的循环次数
format long %为提高精度，保留更多位数
for i = 1 : max
    x1 = interation(x);
    x2 = interation(x1);
    x3 = x2 - (x2 - x1) ^ 2 / (x2 - 2 * x1 + x);
    error = abs(x3 - x);
    x = x3;
    errors(i) = error;
    if error < stopError, break, end
end
time = i;
ans = rad2deg(x); %转换成角度
end

输入命令[errorsA, ans, time] = aitken(0, 50, 1.7e-5)求解得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
errorsA =

   0.399614867056990   0.000235879375045   0.000000000176165


ans =

  22.909760215804827


time =

     3

可以看到，Aitken加速迭代法仅需3次迭代就得到了符合条件的解，且它的迭代误差只用$0.000000000176165$，小于上述所有的方法，由此该方法的优势得以体现。

Newton迭代法

Newton迭代法也是一种求解非线性方程的高效算法，因此我也对其进行实现。
这里要用到func的导数，经计算，编写func的导函数为程序df：

1
2
3
4
5
6
function [y] = df(x)
%求导数
%统一使用弧度制
format long
y = (0.75 * sin(x) / (1 - (1 / (1.878 + 0.75 * cos(x))) ^ 2) ^ 0.5) / (1.878 + 0.75 * cos(x)) ^ 2 - 1;
end

Newton迭代法

编写Newton迭代法的计算程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function [errors, ans, time] = newton(x, max, stopError)
%Newton迭代法
%func是待求零点的函数
%x是初始点
%max是最多循环步数，防止死循环
%stopError是预定精度，作为终止条件
%errors记录每次循环的误差
%ans记录最终求解结果，表示为角度
%time是总的循环次数
format long %为提高精度，保留更多位数
for i = 1 : max
    o = x - func(x) / df(x);
    error = abs(o - x);
    x = o;
    errors(i) = error;
    if error < stopError, break, end
end
time = i;
ans = rad2deg(x); %转换成角度
end

输入命令[errorsN, ans, time] = newton(0, 50, 1.7e-5)进行计算，得解：

1
2
3
4
5
6
7
8
9
10
11
12
13
errorsN =

   0.390355832559508   0.009488988787132   0.000005925259246


ans =

  22.909760215672179


time =

     3

Newton下山法

为尽可能避免因初值选取不当导致计算过程缓慢收敛或者发散（经上面计算，此问题不存在这种情况），引入下山因子$\lambda \in (0,1]$，得到改进后的Newton下山法，其计算程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function [errors, ans, time] = hill(x, max, stopError)
%Newton下山法
%   此处显示详细说明
format long %为提高精度，保留更多位数
l = 1;
for i = 1 : max
    o = x - l * func(x) / df(x);
    while abs(func(o)) > abs(func(x)) %不满足下山条件
        l = l / 2;
        o = x - l * func(x) / df(x);
    end
    error = abs(o - x);
    x = o;
    errors(i) = error;
    if error < stopError, break, end
end
time = i;
ans = rad2deg(x); %转换成角度
end

计算得到结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
errorsH =

   0.390355832559508   0.009488988787132   0.000005925259246


ans =

  22.909760215672179


time =

     3

由于此问题初值选取得当，即初值取$0$时使用一般Newton迭代法不存在缓慢收敛或者发散的问题，因此Newton下山法在这里并没有发挥作用。可以看到，Newton迭代法仅$3$步就完成了求解的任务，非常高效。

问题的解

以上方法都得到了一致的答案，根据精度要求，我们得出此条件下功率角$\theta$为$22.910^{\circ}$，与许实章编《电机学习题集》中的例题答案$22.9^{\circ}$相吻合。

方法比较

将上述各种方法的误差记录绘制成图表，由于Newton下山法在该问题中没有发挥作用，因此仅作出Newton迭代法的迭代误差图像。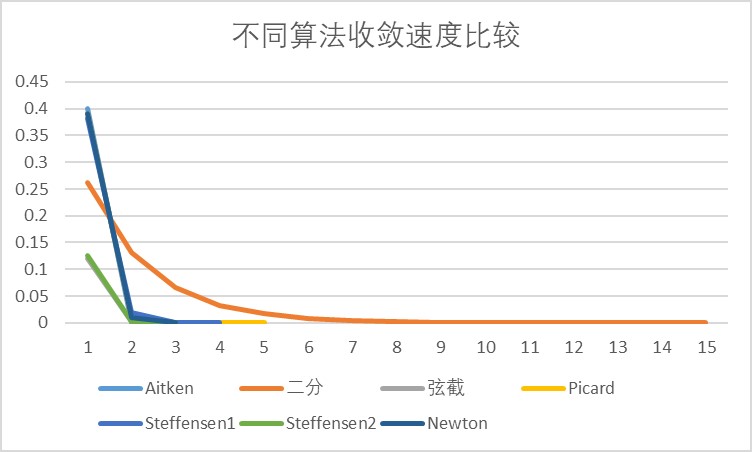

根据图片，我们可以观察到以上各个方法均收敛。其中，表现较为优越的有Aitken加速迭代法、Newton迭代法和Steffensen迭代法，均用了$3$次迭代就达到了精度要求。然而这里Steffensen法的收敛速度更依赖于初值的选取，当初值选为$0$时，它的收敛速度就类似于弦截法在该问题上的收敛速度了。因此，总的来说，对于这个问题，最高效的算法是Aitken加速迭代法和Newton迭代法。另外，二分法最简单却也最低效，迭代了$15$次才达到预设的精度要求。可见，各种算法的效率大致上与它们的复杂度和高级程度成正比关系。

碰到底线咯 后面没有啦

本文标题:matlab笔记：一个非线性方程问题的多种求解方法

文章作者:高深远

发布时间:2019年11月16日 - 00:35

最后更新:2020年02月07日 - 17:31

原始链接:https://gsy00517.github.io/matlab20191116003545/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

0%