线性代数中的正则化

如果直接搜索正则化这个名词，首先得到的一般是代数几何中的一个概念。
百度词条对它的解释是：给平面不可约代数曲线以某种形式的全纯参数表示。
怎么样？是不是觉得一头雾水。
这里我推荐使用谷歌或者维基百科来查询这些专业名词。

对于不能科学上网的朋友，没关系，我这里提供了谷歌镜像和wikiwand，大家可以在上面得到一样的搜索结果。

我们直接到维基百科搜索regularization：
里面第一段是这样解释的：In mathematics, statistics, and computer science, particularly in machine learning and inverse problems, regularization is the process of adding information in order to solve an ill-posed problem or to prevent overfitting.
这就和我们在机器学习应用中的目的比较相近了。

机器学习中的正则化

在机器学习中，正则化是一种为了减小测试误差的行为（有时候会增加训练误差）。
我们在构造机器学习模型时，最终目的是让模型在面对新数据的时候，可以有很好的表现。当你用比较复杂的模型比如神经网络去拟合数据时，很容易出现过拟合现象（训练集表现很好，测试集表现较差），这会导致模型的泛化能力下降，这时候，我们就需要使用正则化，来降低模型的复杂度。
为了加深印象，我下面简单介绍几种常用的机器学习正则化方法：

早停法（Early Stopping）
早停法，就是当训练集的误差变好，但是验证集的误差变坏（即泛化效果变差）的时候停止训练。这种方法可以一定程度上有效地防止过拟合，同时这也说明了验证集在机器学习中的重要性。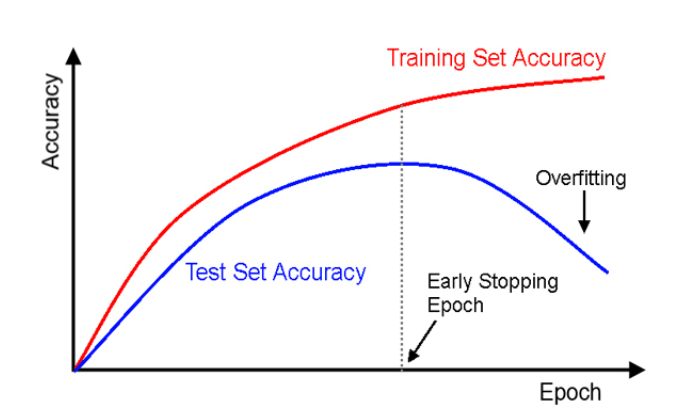
权重正则化法
因为噪声相比于正常信号而言，通常会在某些点出现较大的峰值。所以，只要我们保证权重系数在绝对值意义上足够小，就能够保证噪声不会被过度响应，这也是奥卡姆剃刀原理的表现，即模型不应过度复杂，尤其是当数据量不大的时候。
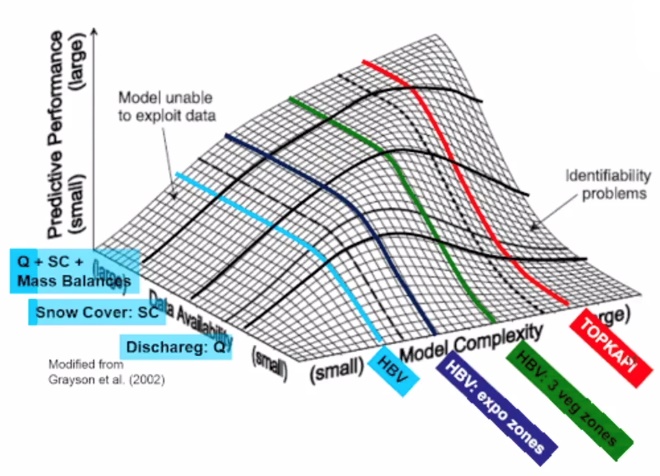
上面是在一个网课上看到的、我觉得可以较好地呈现模型的复杂度与数据量对模型预测表现的影响的一张图片，其中向左的横轴表示数据量大小，向右的横轴表示模型复杂度，竖轴是预测表现。通过这张图，可以很明显地观察到：模型的复杂度提升需要大量的数据作为依托。
权重正则化主要有两种：
- L1正则：$ J=J_{0}+\lambda \left | w \right |_{1} $，其中J代表损失函数（也称代价函数），$ \left | w \right |_{1} $代表参数向量w的L1范数。
- L2正则（weight decay）：$ J=J_{0}+\lambda \left | w \right |_{2} $，其中$ \left | w \right |_{2} $代表参数向量w的L2范数。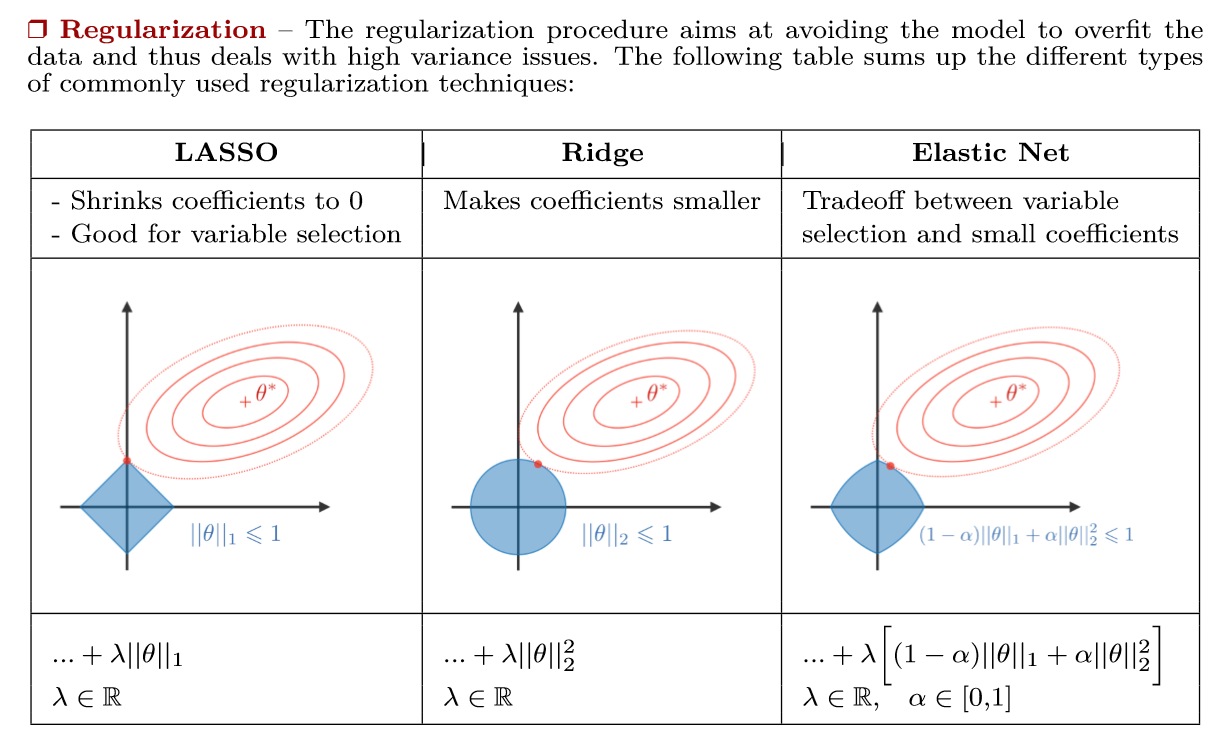这里就产生了Lasso回归与岭回归两大机器学习经典算法。其中Lasso回归是一种压缩估计，可以通过构造惩罚函数得到一个较为精炼的模型，使得它可以压缩一些系数，同时设定一些系数为0，从而达到特征选择的目的。基于Lasso回归这种可以选择特征并降维的特性，它主要有这些适用情况：
1. 样本量比较小，但指标量非常多的时候（易于过拟合）。
2. 进行高维统计时。
3. 需要对特征进行选择时。
  对于这些回归的详细解释，大家可以到网上搜集相关信息。
  补充：
  L0范数：向量中非零元素的个数。
  L1范数：向量中每个元素绝对值的和。
  L2范数：向量元素绝对值的平方和再开方。
下面我再附上一组图，希望能帮助更好地理解权重正则化：
首先我们可视化一个损失函数。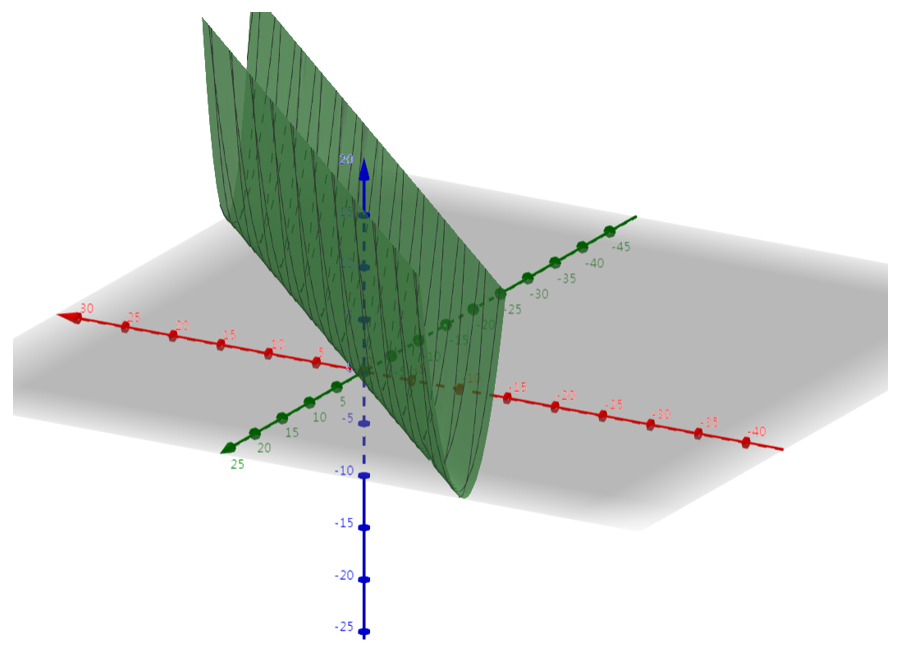
下面我们看一看正则化项的图示，这里使用L1范数作为正则化项。
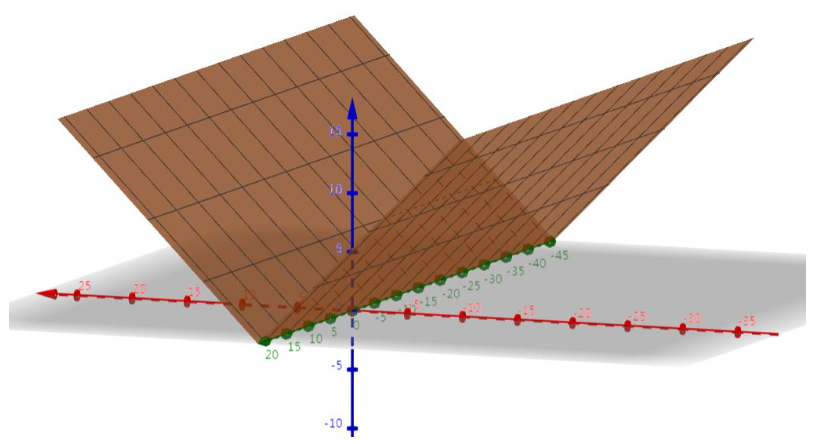
接着，我们将上面两者线性组合：
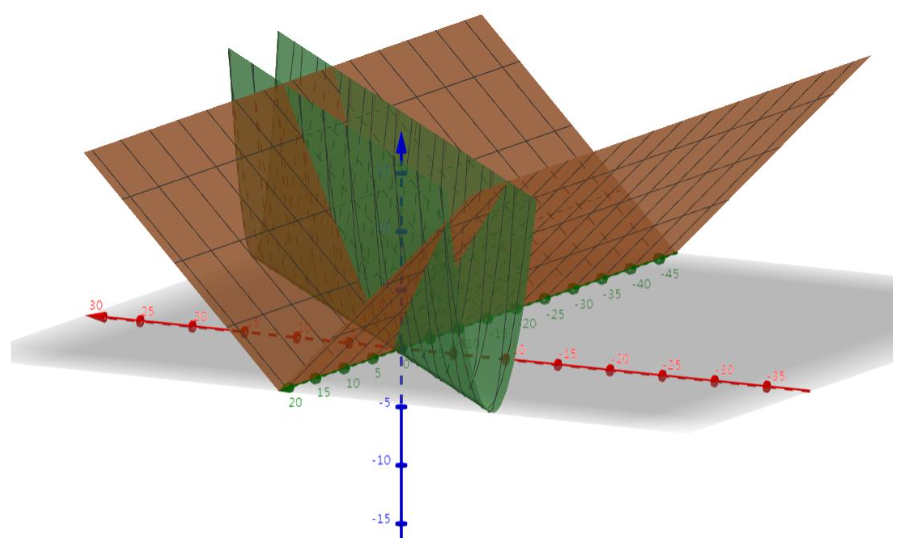
我们来看看结果：
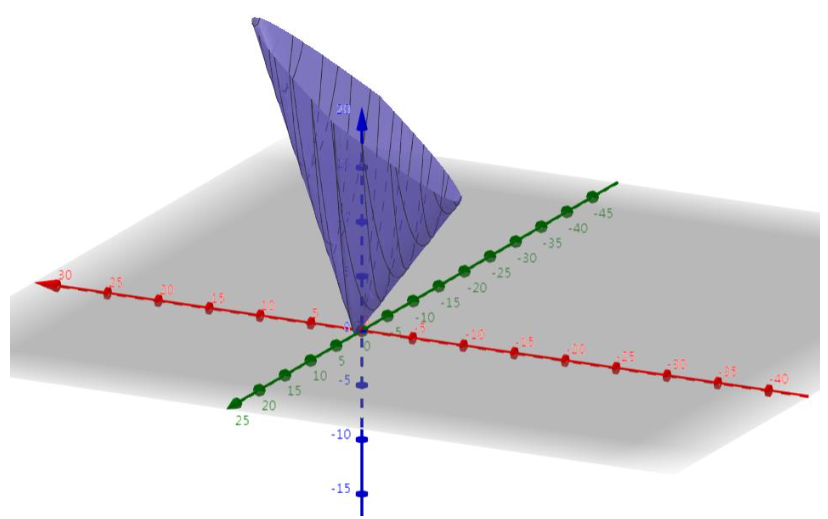
可见，正则化项的引入排除了大量原本属于最优解的点，上图的情况中剩下一个唯一的局部最优解。
正则化项的引入，除了符合奥卡姆剃刀原理之外。同时从贝叶斯估计的角度看，正则化项对应于模型的先验概率，即相当于假设复杂的模型具有较小的先验概率，而简单的模型具有较大的先验概率。
数据增强
数据增强可以丰富图像数据集，有效防止过拟合。这种方法在AlexNet中有很好的应用，大家可以看看我的博文deep-learning笔记：开启深度学习热潮——AlexNet。
随机失活（dropout）
dropout即随机砍掉一部分神经元之间的连接，每次只更新一部分，这可以有效地增加它的鲁棒性，提高泛化能力。这个方法在AlexNet中也有详细的解释，推荐大家去看一下。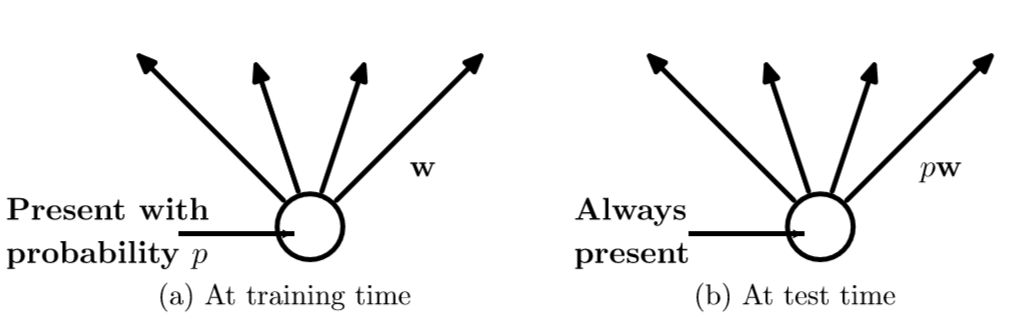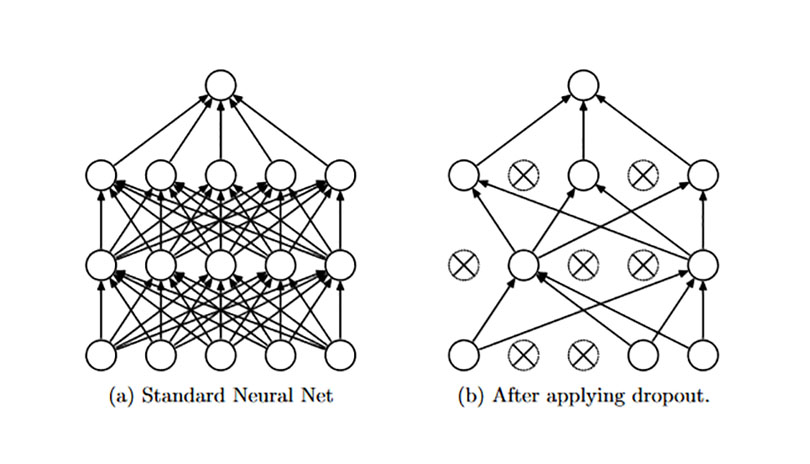以上就是比较常规且流行的正则化方式，今后或许会有补充，也欢迎大家提供意见~